Аппроксимация, устойчивость разностных схем. Вычислительные алгоритмы. Устойчивость и сходимость

Дальневосточный Федеральный Университет

Инженерная школа

Кафедра: Прикладная механика и математическое моделирование

Специальность: Прикладная механика

Курсовая работа по курсу

Современные численные методы

Тема: «Аппроксимация, устойчивость разностных схем»

                                                      Выполнил: :

                                                                           Проверил: профессор  

г. Владивосток

2013 г.

Содержание

Введение                                                                                                                         3

Основная часть:

-   Постановка смешанной задачи                                                                                4

-   Разностные схемы                                                                                                                                                                                    

-   Аппроксимация                                                                                                         7

-   Вычислительные алгоритмы                                                                                    9

-   Устойчивость и сходимость                                                                                     10

-   Метод Фурье, применительно к решению задачи                                                 13

Практическая часть:

-   Аналитическое решение                                                                                           16

-   Численное решение                                                                                                   22

Список литературы                                                                                                        25

Введение

Данная работа посвящена рассмотрению и анализу теоретических основ и решения краевых тепловых задач методом прогонки.

Актуальность темы обусловлена тем, что решение задач таким способом делается математически, а не физическими уравнениями.

Цель работы – рассмотреть метод и решить наглядно уравнение.

Теоретической и методологической основой исследования, информационной базой являются труды крупнейших мыслителей в рассматриваемой области, таких  как: Е. А. Волков, А. А. Самарский, Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков, результаты практических исследований видных отечественных и зарубежных авторов, посвященных тематике "Численные методы", справочная литература, прочие актуальные источники информации.

В процессе исследования применялись следующие методы:  изучение и анализ теоретического и практического материала по данной теме.

Работа имеет традиционную структуру и включает в себя введение, основную часть, состоящую из 3 глав, заключение и библиографический список. Во введении обоснована актуальность выбора темы, поставлены цель исследования, охарактеризованы методы исследования и источники информации. В основной части рассмотрена теоретическая информация о методе, определяются основные понятия. Так же имеет место практический характер и на основе отдельных данных делается анализ метода.

Постановка смешанной задачи.

Пусть

т. е.  — замкнутый прямоугольник,  — полуоткрытый прямоугольник. Требуется найти непрерывную на замкнутом прямоугольнике  функцию и(х, t), которая на  удовлетворяет уравнению теплопроводности

(1)

при t = 0 удовлетворяет начальному условию

(2)                а при х = 0 и х = 1 подчиняется краевым условиям

u(0,t)=p(t), u(l,t)=q(t),                                             (3)

где f(x,t), s(x), p(t), q(t) — заданные достаточно гладкие функции, причем s(0)=p(0), s(l)=q(0).

Задача (1) — (3) называется смешанной, поскольку она содержит как начальное условие, так и краевые условия. Известно, что у поставленной задачи существует единственное решение и(х,t). Мы будем предполагать, что это решение имеет на замкнутом прямоугольнике  непрерывные частные производные du/dt, d²u/dt², д²и/дх, .

Сетки и нормы. Пусть h = 1 /N, τ= Т/М — шаги по х и t, где N, М — натуральные, = kh, ,. Построим сетки (рис. 22)

 

Сетка состоит из узлов сетки , обозначенных на рис. 22 крестиками. Эти узлы расположены на трех сторонах прямоугольника ,на которых заданы начальное и краевые условия. Сетка состоит из остальных узлов сетки . Зададим для сеточных функций, определенных на  или на , следующие нормы:

                        (4)

Разностные схемы

Введем разностный оператор :

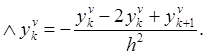                                                                                                     ₍₅₎

Здесь под выражением подразумевается значение сеточной функции  в точке (x_k, t_v), т. е.

 

 

 

 

 

 

 

 

 

 

 

_Рис.1

 

Скобки опущены для упрощения записи. Аналогичные упрощения в записи будем допускать и при введении других операторов.

Зададим на сетке тождественный оператор

                                                   ₍₆₎

_{и сеточную функцию}

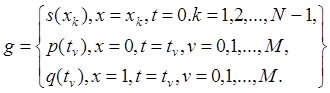                                                                                 ₍₇₎

_{Рассмотрим две разностные схемы}                                                                         

                                                            (8)

(9)

(10)                          

                                                                                                          (11)

Здесь и далее k = 1, 2, ..., N— 1, a ν = 1, 2, ..., M.

Шаблоны разностных уравнений (8), (10) представлены соответственно на рис. 2, 3. Обе разностные схемы (8), (9) и (10), (11) называются двухслойными, так как шаблоны разностных уравнений

Рис. 2                                                                  Рис.3

(8) и (10) содержат узлы, лежащие только на двух слоях — подмножествах сетки , отвечающих значениям времени t =  и t = t_v.

Слой, находящийся на горизонтальной прямой t=t_v-1, называется нижним, а другой — верхним. Разностные схемы (8), (9) и (10), (11) отличаются тем, что в уравнении (8) оператор  действует на нижнем слое, а в уравнении (10) оператор  вынесен на верхний слой и, кроме того, значения правой части  и  берутся на разных слоях. Ограничимся пока сделанным формальным описанием двух разностных схем. Их качественное различие выяснится ниже.

Аппроксимация

Сопоставляя, с одной стороны, дифференциальное уравнение (1), а с другой стороны, разностные уравнения (8) и (10), видим, что частной производной u'_t отвечает разностная производная  , а частной производной — соответствует разностная производная второго пор ял- ка в направлении х, образуемая с противоположным знаком с помощью оператора  (см. (5)).

Пусть и (х,t)— решение задачи (1) —(3). Поскольку его частные производные d²u/dt², по предположению непрерывны и, следовательно, ограничены на замкнутом прямоугольнике , то согласно (5), (10.3), (10.1)

                                           (12)

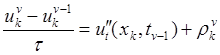                                          (13)

Где k=1,2,…N-1,v=1,2,…,M,  

                                                   (14)

и  — некоторые постоянные, не зависящие от h, τ, k, v.

В силу непрерывности частных производных u'_t, и"_хx на  решение задачи (1) — (3) удовлетворяет уравнению (1) на замкнутом прямоугольнике . Следовательно, выполняется равенство

                              (15)

для k = 1, 2, ...,N — 1, v = 1, 2, ..., М, т. е., в частности, и для t_v-1 = 0.     Согласно (12), (13), (15) невязка –ψ1 решения u задачи (1) — (3) для разностного