Методы теории возмущений. Бифуркации., страница 9

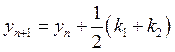
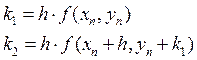
Аналогично для 4-го порядка:

Устойчивость схемы Рунге-Кутты

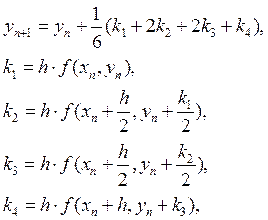
Устойчивость схемы чаще всего исследуется на модельных задачах:

;

Решение этого уравнения:

;

В общем виде:

 - неоднородное разностное уравнение

;  - соответствующее однородное (характеристическое) уравнение.

 - решение этого уравнения.

Для того, чтобы решение было устойчивым, желательно, чтобы , полученное по схеме Рунге-Кутты, совпадало с аналитическим с точностью до , где  - порядок аппроксимации.

; ;

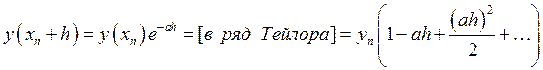
Т.е. каждое последующее значение будет меньше предыдущего и значит требование устойчивости будет выполняться. Погрешность будет вести себя «правильно»: расти при  (также как и решение) и убывать при . Следовательно, схемы Рунге-Кутты устойчивые.

Порядок точности метода Рунге-Кутты

Как получить возможность оценить погрешность численного решения не имея аналитического?

Пусть  - аналитическое или точное решение, а  - приближенное решение задачи , полученное по схеме Рунге-Кутты. Обозначим за  - решение с шагом , а за  - с шагом . Оценим погрешность Рунге-Кутты 4-го порядка:

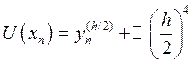
Вычитая, получим: 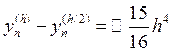. Тогда погрешность метода Рунге-Кутты (а она пропорциональна ) вычисляется: 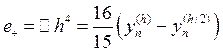, т. е. решив одну задачу на разных сетках можно оценить погрешность.

Выводы: решение задачи Коши можно представить в виде:

                          

 - функция, которая определяется:

1)  правой частью уравнения

2)  способом построения численного метода

3)  способом разбиения участка интегрирования, т. е. построением сетки.

При  и  метод решения задачи Коши называется одношаговым, т. е. вычисления на каждом шаге при  производится по одному вычислению. При  и  метод называется многошаговым. В этом случае дискретный аргумент изменяется от  до . Возникает необходимость в дополнительных правилах вычисления первых значений  и последних  значений . Одношаговые и многошаговые методы называются явными, если  и неявными, если .

Методы прогноза и коррекции

                                                

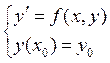
Пусть дана задача Коши . Под решением этой задачи понимаем кривую , тангенс угла наклона к которой в каждой точке  задается уравнением задачи -  это локальное свойство. Распространение этого локального свойства на всю область определения и означает решение уравнения. Естественно, что решением уравнения является не одна кривая, а через любую точку  проходит решение уравнения .

Если мы хотим получить единственное решение, проходящее через заданную точку, то естественно начать вычислительный процесс следующим образом: для заданной точки   вычисляем тангенс угла наклона  и движемся в этом направлении на «небольшое» расстояние, выбираем следующую точку; затем, используя эту точку как начальную, повторяем процесс.

Этот удобный и простой метод тем не менее не лишен ряда недостатков, например, для строго возрастающего решения задачи численное решение будет заметно меньше аналитического. Такой результат определяется тем, что для получения следующей точки используется тангенс угла наклона касательной в предыдущей точке. Чтобы избежать такой ошибки можно изменить вычислительный процесс: сначала вычислить тангенс угла наклона касательной в последующей точке, а затем продолжить движение в направлении некоторой линейной комбинации (например, полусуммы) начального и конечного тангенсов угла наклона. Т.о. весь вычислительный алгоритм разбивается как бы на два этапа: 1) прогноз (дальнейшего движения); 2) коррекция выбранного направления с учетом предыдущего значения .

Для вычисления значения в последующей точке применяется формула простого прогноза:

                                              в которой применяем тангенс угла наклона в середине удвоенного интервала.

Таким образом, мы предсказываем, каким может быть . В качестве корректирующей применяется формула простой коррекции:

                                       

Оценка погрешности аппроксимации

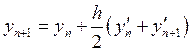
Сокращая формулу