Методы теории возмущений. Бифуркации., страница 3

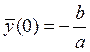Если  произвольным образом, то при любых  решение  предела не имеет и будет неограниченным. Если даже условия, наложенные на  и  выполнены, то предельный переход имеет место только при . (Т.к. при  имеем ; , но ).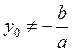

Уравнения (1), (3) называются уравнениями с малым параметром при старших производных. Рассмотрим систему ДУ:

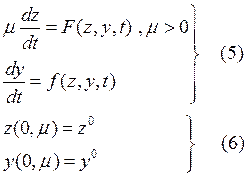
Любое уравнение второго порядка можно привести к (5), (6).

Правые части в (5) полагаем непрерывными вместе с частными производными по и в некоторой области . Пусть в (5) . Тогда

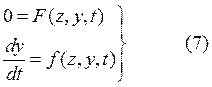
(7) – вырожденная система. В общем случае она может иметь несколько решений. Предположим, что все решения (корни) этого уравнения действительны и изолированы в . Корень  называется устойчивым в замкнутой области , если

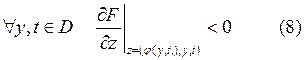
Выберем , удовлетворяющий (8) и подставим во второе уравнение системы (7):

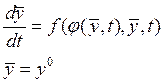
Рассмотрим частный случай:

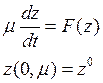
Тогда

 - будет являться вырожденным уравнением

Пусть   – решение вырожденного уравнения – устойчивый корень области .

Условие устойчивости (8) примет вид:

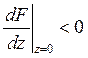
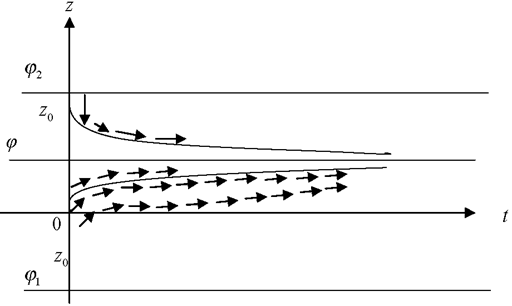
Пусть  и  - тоже решения, причем один из них , а второй . Построим поле направлений для уравнения

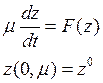
Пусть кроме этого . При малом  касательные к интегральным кривым идут почти параллельно оси , за исключением, может быть, малой окрестности корней вырожденного уравнения. Так как 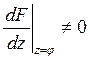, то  - простой корень и при  происходит смена знака . Пусть . Рассмотрим -окрестность корня , . Интегральные кривые, начинающиеся в точке  будут резко идти вверх при  и, соответственно, вниз при  и, достигнув , интегральные кривые выходить из нее не будут при условии, что  мало. Это и означает, что решение системы

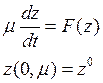
будет достаточно близким к решению  для всех  кроме некоторой окрестности .

Вывод: из этой геометрической интерпретации видно, насколько важна принадлежность начального значения  заданному промежутку  (области влияния корня ). Поскольку, если  ниже , то решение будет притягиваться к корню .

Теорема Тихонова

При выполнении следующих условий:

1. Правая часть системы (5) непрерывна вместе с  и  в области .
2. Функция  непрерывна вместе с  в области .
3.  - устойчивый корень вырожденной системы (7).
4. Решение вырожденной задачи (7) определено для  и .
5. Начальное значение  принадлежит области влияния корня , где  - решение уравнения.

Тогда решение задачи (5) и (6) существует, и на отрезке  имеет место предельный переход:

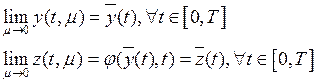
Доказательство.

1.  Рассмотрим окрестность в точке  и сделаем в уравнении

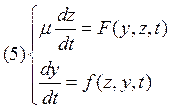
замену 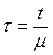. Соответственно, получим систему

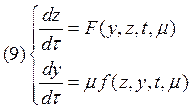
с соответствующими начальными условиями .

На любом конечном промежутке изменения переменной систему (9) можно рассматривать как регулярную возмущенную систему

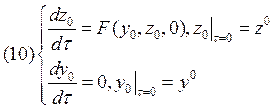
В системе (10) последнее уравнение можно разрешить , а соответствующее уравнение от  примет вид: .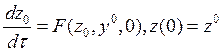

А это последнее уравнение аналогично уже исследованной задаче вида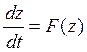 и для этой задачи существует устойчивый корень, т.е. существует такое   , что  будет справедливо: 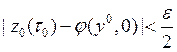 (определение устойчивости корня).

Сравним задачи (10) и (9). Из первого условия теоремы следует выполнение условия о регулярном возмущении , где  может быть сколь угодно велико и фиксировано.

Решение невозмущенной задачи (10) определено , и, в частности, на отрезке , тогда мы получаем, что  и при достаточно малых  на отрезке  или на аналогичном отрезке  существует решение задачи (9) или решение задачи (5) 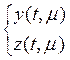, причем для этих решений существует неравенство   .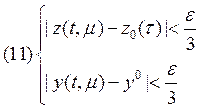

Поскольку  - устойчивый корень, а функция  непрерывна, то при условии, что  можно получить следующее неравенство: 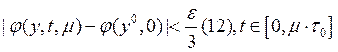. Из неравенств (11) и (12) мы получаем, что при   у нас будет выполнятся, что .

Т.е.  будет устойчивым корнем для .

2.  Обозначим разность . Из неравенства (13) следует, что  будет сколь угодно малым при  . Неравенство (13) будет выполнятся в некоторой окрестности справа от точки . Величина этой окрестности заранее не определена, но в этой окрестности  близко к решению . Покажем это.