Методы теории возмущений. Бифуркации., страница 7

u=j(x₁,…,x_n) непрерывно дифференцируема в области G. У функции u существует частные производные по всем переменным x₁,…,x_n и 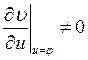 в G, тогда u будет решением исходного квазилинейного уравнения.

Доказательство.

По соответствующей теореме о неявной функции можно записать:

                    (**)

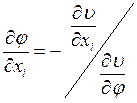Исходное квазилинейное уравнение имеет вид

                   (*)

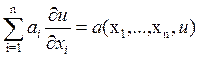Так как u=j, то (**)à(*), тогда

.

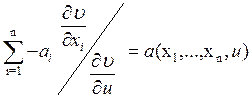Умножаем последнее на  и перенесем все в правую часть. Получим (1). Ч.и.т.д.

На этой теореме базируется алгоритм решения квазилинейных задач (*):

1. Необходимо выписать систему ДУ, которая определяет характеристики уравнения (*).

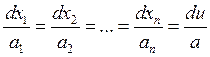                 (2)

Интегральная кривая системы (2), то есть характеристики уравнения (*) будем называть характеристиками квазилинейного уравнения. Если уравнение (1) и его коэффициенты удовлетворяют всем ограничениям (все коэффициенты одновременно не равны нулю), то тогда это означает, что характеристики заполняют область D: (x₁,…,x_n, y) и через каждую точку этой области проходит одна и только одна характеристика.

2. Строим общее решение линейного уравнения (1). Получаем n независимых первых интегралов от аргументов x₁,…,x_n, u.   y_i(x₁,…,x_n,u), i=1,…,n и некоторую функцию u.

       (3)      

3. Полагаем u=0.

                     (4)

Это уравнение определяет функцию u, которая и будет решением исходного квазилинейного уравнения (*).

Пусть интегральная поверхность нам не известна, но известны все характеристики. Тогда, если мы сумеем «склеить» из характеристик интегральную поверхность, то восстановленная поверхность u будет интегральной поверхностью, так как вектор, состоящий из коэффициентов (a₁,…,a_n,a)^T квазилинейного уравнения, будет касательным к каждой характеристике (по построению), а по определению, он должен быть касательным к интегральной поверхности, следовательно, он будет ортогонален нормальному вектору

.

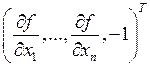То есть их скалярное произведение будет равно нулю, а это скалярное произведение и есть уравнение (*).

Численные методы решения начальной задачи (задачи Коши)

Пусть дана задача Коши

                                                               

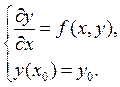
Построим приближённое решение задачи (1) и (2), определённое лишь в конечном числе точек  отрезка .

Множество точек  , на котором ищется приближённое решение задачи (1) и (2), называется сеткой.

Точки  - узлы сетки, а величина  - шаг сетки. Если , то сетка называется равномерной, иначе неравномерной. Функция дискретного аргумента , определённая лишь в узлах сетки, называется сеточной функцией. Для определения сеточной функции, которая является решением задачи (1) и (2), должна быть задана некоторая разностная схема:

-  система уравнений, связывающих между собой значения сеточной функции ,

-  заданные дополнительные условия (2),

-  значения правой части  в узлах сетки.

Запишем исходную задачу в общем виде:

                                            (3).

Тогда соответствующая ей разностная схема (задача) имеет вид:

,                                           (4)

где       - дифференцируемый оператор,

 - разностный оператор,

 - сеточная функция,

 - решение задачи (3),

 - значение правой части  в узлах сетки.

Задача определения сеточной функции  должна быть построена так, чтобы при  сеточная функция сходилась в определённом смысле к решению исходной задачи (3).

Будем говорить, что семейство сеточных функций  сходится к точному решению  задачи (3), если

 при ,                       (5)

где  - значение точного решения задачи (3) в узлах сетки.

Если, кроме того,   такой, что  выполняется неравенство:

,                            (6)

где  и  - константы, не зависящие от , то говорят, что имеет место сходимость порядка .

Разностная схема должна обладать свойствами исходной задачи, так как исходная задача – математическое описание некоторого физического процесса.