Методы теории возмущений. Бифуркации., страница 17

1)  Если , где  – положительно определённый симметричный оператор, то  функционал энергии -                     

2)  Если , то  функционал наименьших квадратов -  

3)  , функционал обобщённых наименьших квадратов –

 

Замечание

За счет выбора постоянной C в функционале можно сделать так, чтобы вид функционала , совпадал с соответствующим функционалом ошибки. При этом в функционалах , оператор A не обязан быть симметричным.

Минимум функционала энергии. Решение уравнения с самосопряжённым оператором. Обобщённые решения.

Минимум функционалов , равен нулю при элементе  в каком-то смысле связанном с решением уравнения . Определим с решением какого уравнения связан этот , реализующий минимум функционала . Для этого по теореме Рисса представим , тогда

                                    

Т.е. это некоторый функционал энергии для оператора . Этому функционалу сопоставим операторное уравнение  . Пусть  – симметричный положительно определённый оператор, тогда справедлива теорема:

Теорема. Для того, чтобы некоторый элемент  доставлял минимум функционалу с самосопряженным положительно определённым оператором  необходимо и достаточно чтобы этот  удовлетворял .

Доказательство:

Достаточность: рассмотрим некоторый : .  

                      

Если  – решение операторного уравнения , тогда в соотношении выберем  и получим .

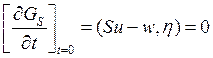Необходимость: если  доставляет минимум  и ,тогда подставим элемент  в и получим .  выполняет роль параметра. Т.к.  доставляет минимум , то при – минимум , то  – функция скалярного элемента  и поиск минимума - . Т.е. минимум при =0.

Замечание

Если оператор  не самосопряжённый, а только симметричный и положительно определённый, то   тоже достигает своего минимума, но уже на элементе ( возможно ). Тогда  – обобщённое решение . Чаще всего для определения обобщённого решения используют равенство . Обобщённым решением будем называть элемент u:

                                                                                

Т.к. u – обобщённое решение и доставляет минимум энергетическому функционалу, то уравнение типа – вариационное. Важно понять, что задача минимизации функционалов , на специально построенном энергетическом пространстве  и задача определения обобщённого решения уравнения с симметричным положительно определённым оператором являются эквивалентными. Задача минимизации, которая определяется формулой сводится к представлению линейного функционала по теореме Рисса в виде функционала   в пространстве .

Свойства минимизирующих последовательностей

Пусть дана . Эта последовательность будет минимизирующей для квадратичного функционала , если . Тогда если последовательность  минимизирующая для , то в норме .

Вариационные методы минимизации квадратичного функционала. Обобщённый метод Ритца

Пусть дан функционал ошибки  и пусть  - полная в пространстве H_s линейно независимая система элементов. Тогда - линейная оболочка, 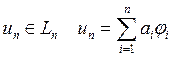 . Тогда вместо задачи минимизации функционала на всём H, будем рассматривать минимизацию на  полагая, что при больших n решения этих двух задач будут мало отличаться. Вторая намного проще и она сводится к решению СЛАУ. Т.е. если мы подставим соотношение в выражение для функционала , то . В точке минимума этой функции будет выполняться

                                            

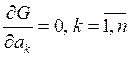
Теперь применим к :                              

Подставляя в получим систему уравнений для определения решения u_n

                                

                                       

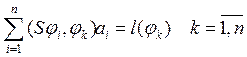
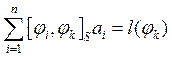
Для функционала в форме :                                                                                                 

Система уравнений - это система уравнений обобщённого метода Ритца для приближения минимизирующего функционала или для определения приближенного решения уравнения , а при  определения приближенного решения . Для всех систем уравнений - можно сформулировать следующие утверждения: