В функциональном пространстве гладких векторных полей на компактном многообразии открытое, всюду плотное множество образует поле, все особые точки которого – невырожденные, т.е. изолированы. Вырожденная точка распадается на невырожденные при сколь угодно малом шевелении поля.
Пусть ![]() – фазовое пространство некоторого
физического процесса,
– фазовое пространство некоторого
физического процесса, ![]() – некоторое начальное состояние
процесса. Обозначим состояние процесса в момент времени
– некоторое начальное состояние
процесса. Обозначим состояние процесса в момент времени ![]() при
начальном состоянии
при
начальном состоянии ![]() как
как![]() . Таким образом, мы определили для любого вещественного
числа
. Таким образом, мы определили для любого вещественного
числа ![]() отображение
отображение ![]() . Это
отображение называется отображением за время
. Это
отображение называется отображением за время ![]() .
.
Фазовым
потоком называется пара ![]() , составленная из
множества
, составленная из
множества ![]() (фазовое пространство) и
однопараметрической группы
(фазовое пространство) и
однопараметрической группы ![]() (группы
преобразований множества
(группы
преобразований множества ![]() ). Другими словами, фазовый
поток – математическая модель некоторого детерминированного процесса.
). Другими словами, фазовый
поток – математическая модель некоторого детерминированного процесса.
Пусть ![]() - фазовая точка. Рассмотрим отображение
- фазовая точка. Рассмотрим отображение ![]() (в наших обозначениях
(в наших обозначениях ![]() ). Фазовой кривой потока
). Фазовой кривой потока ![]() будет называться образ отображения
будет называться образ отображения ![]() , т.е. фазовая кривая – некоторое
подмножество фазового пространства.
, т.е. фазовая кривая – некоторое
подмножество фазового пространства.
Положением
равновесия или неподвижной точкой ![]() потока
потока ![]() называется фазовая точка, являющаяся
фазовой кривой, т.е.
называется фазовая точка, являющаяся
фазовой кривой, т.е. ![]() .
.
Фазовой
скоростью ![]() потока
потока ![]() в точке
в точке ![]() называется
вектор скорости движения фазовой точки
называется
вектор скорости движения фазовой точки 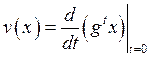 т.е.
векторное поле
т.е.
векторное поле ![]() на множестве
на множестве ![]() сопоставляет каждой точке множества
сопоставляет каждой точке множества ![]() исходящий из этой точки вектор
исходящий из этой точки вектор ![]() .
.
Точка, в которой вектор векторного поля обращается в ноль, называется особой точкой.
Пусть
множество особых точек семейства – гладкая кривая. Значение параметра, которому
соответствует вырожденная особая точка, называется бифуркационным значением
параметра, а сама вырожденная точка в прямом произведении фазового пространства
на ось значений параметра (т.е. точка в ![]() -мерном пространстве) называется бифуркационной
точкой.
-мерном пространстве) называется бифуркационной
точкой.
Рассмотрим
значение параметра ![]() как функцию, заданную на кривой
особых точек. Тогда бифуркационные значения параметра – критические значения
этой функции, а бифуркационные точки – критические точки соответствующей
функции (т.е. точки, где дифференциал этой функции равен нулю).
как функцию, заданную на кривой
особых точек. Тогда бифуркационные значения параметра – критические значения
этой функции, а бифуркационные точки – критические точки соответствующей
функции (т.е. точки, где дифференциал этой функции равен нулю).
Критическая точка называется невырожденной, если второй дифференциал функции в этой точке не вырожден, а соответствующая бифуркационная точка называется невырожденной бифуркационной точкой.
Бифуркационное значение параметра называется регулярным, если ему соответствует ровно одна невырожденная бифуркационная точка.
Методы теории возмущений................................................................................................................................... 2
Методы теории возмущений................................................................................................................................... 2
Теорема Тихонова..................................................................................................................................................... 6
Уравнения в частных производных первого порядка....................................................................................... 9
Численные методы решения начальной задачи (задачи Коши)................................................................... 14
Метод Эйлера........................................................................................................................................................... 16
Модификации метода Эйлера............................................................................................................................... 16
Методы Рунге-Кутты.............................................................................................................................................. 16
Устойчивость схемы Рунге-Кутты....................................................................................................................... 17
Порядок точности метода Рунге-Кутты............................................................................................................. 18
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.