Методы теории возмущений. Бифуркации., страница 12

Общее решение задачи (1), содержащее быстро меняющуюся/жесткую/ и медленно меняющуюся/гладкую/ компоненту может быть удовлетворительно аппроксимировано численным решением, найденным по неявной схеме.

Рассмотрим систему линейных ДУ

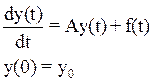     (5)

А- постоянная матрица A[n][n]

Жесткость для задачи (5) определяется условиями, которым должна удовлетворять А, точнее ее собственные значения

С точки зрения свойств матрицы A жесткие задачи можно определить следующим образом.

Задачу (5) можно назвать ЖЕСТКОЙ, если:

1)  существуют , для которых ;

2)  существуют  умеренной величины, т.е.  «мал» по сравнению с абсолютными величинами собственных значений, удовлетворяющих пункту 1;

3)  не существуют  с «большой» положительной вещественной частью;

4)  не существует  с «большой» мнимой частью, для которого не выполняется условие .

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ УСТОЙЧИВОСТИ

Рассмотрим неявный одношаговый метод Рунге-Кутты  для задачи Коши.

                   (1)

Будем полагать, что для любых  решение данной задачи существует и единственно, а значит, может быть определено с заданной точностью. Устойчивость решения задачи Коши – это некоторое собирательное свойство, которое касается чувствительности к возмущениям конкретной задачи в процессе ее решения. В широком смысле устойчивость означает, что разность между двумя любыми численными решениями, определяемыми формулой (1) для одного и того же шага  остается ограниченной величиной  при конкретном способе определения этой ограниченности.

Существует более сильное свойство, чем устойчивость, которое называется КОНТРАКТИВНОСТЬ. Оно означает, что разность между решениями не возрастает с ростом n. Для того чтобы исследовать устойчивость дискретных аналогов рассмотрим класс жестких задач F, характеризующийся тремя особенностями:

1.  Это тип векторной функции , например, это может быть линейная функция, правая часть соответствующей задачи с постоянными коэффициентами.

2.  Каждому классу Fпринадлежит некоторая функция, такая, что для нее выполняется соотношение

- матрица Якоби для правой части.

- логарифмическая норма матрицы Якоби.

Пусть дана матрица A => логарифмическая норма определяется так

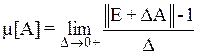
Если норма евклидова, то соответствующая логарифмическая норма может быть вычислена так

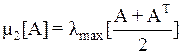
Если , т.е. если  - нормальная матрица.

3.  Класс жестких задач характеризуется нормой, наличие которой следует из пункта 2.

Очень важно, чтобы верхняя оценка функции  для нормы была выбрана независимо от жесткости соответствующего класса задач F. Предположим, что функция  может быть «небольшой» в отличие от классической константы Липшица, которая может быть сколь угодно велика.

Пусть кроме аппроксимации для  и  по методу Рунге-Кутты, который определяется формулой (1) задана еще одна пара аппроксимаций по методу Рунге-Кутты

      (1’)

Величина шага  в формулах (1) и (1’) одна и та же.

Метод (1) называется КОНТРАКТИВНЫМ на классе жестких задач F, если существуют такие вещественные числа , , что для задач из F выполняется:

 и  не зависят от любой величины, на которую может оказать влияние жесткость задачи.

Величина  может быть равна 1. Если , то получаем СТРОГУЮ КОНТРАКТИВНОСТЬ.

При применении этого определения всегда существует некоторая связь между  и , в которую входит оценка логарифмической нормы . В частности,  при  , кроме того, контрактивность зависит и от самой нормы, т.е. при изменении нормы это свойство может быть утрачено.

Метод (1) называется БЕЗУСЛОВНО КОНТРАКТИВНЫМ на F, если существует такое вещественное число , что для любых задач класса F выполняется неравенство:

         (3)

 – не зависит от жесткости задач класса F

Метод (1) называется С-УСТОЙЧИВЫМ на F, если существуют  и  такие, что для любого класса F выполняется неравенство:

                     (4)

Причем  не зависят от жесткости задачи.

Если , то контрактивность по определению (4) соответствует определению 1.