Методы теории возмущений. Бифуркации., страница 14

Разностная схема называется корректной (корректно поставленной), если решение ДУ существует и единственно  и эта схема устойчива, т.е. выполнено .

Немного изменим правую часть/функцию решения: . В силу линейности оператора:

.

                                                                       

Соотношение возможно тогда и только тогда, когда A_h ограничен и существует A^-1.

говорит о том, что малому изменению правой части соответствует малое изменение решения.

Пусть u(x) – точное решение дифференциальной задачи:

                                                                                        

                              

Тогда разностный аналог должен удовлетворять:

                                                                       

                                                                         

Пусть , где z_h – погрешность. Тогда:

                                                                                  

ψ_h в – погрешность аппроксимации на решение . Соответственно

η_h – погрешность аппроксимации краевого условия на решение задачи .

Разностная схема сходится, если .

Разностная схема имеет точность m-ого порядка, или сходится со скоростью , если .

Разностная схема имеет m-ый порядок аппроксимации на решении, если .

Теорема: Если схема устойчива и аппроксимирует исходную задачу, то она сходится!

Д-во: .

Однородные трёхточечные разностные схемы

                                               

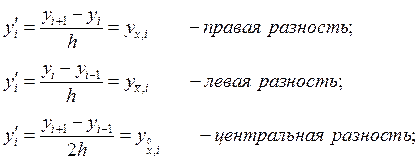
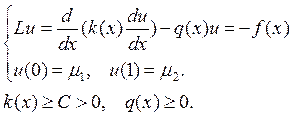
– стационарное распределение температуры в стержне.

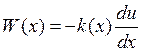– тепловой поток. k(x) – коэффициент теплопроводности.

имеет единственное решение, если  – кусочно-непрерывные функции. Если k(x) претерпевает разрыв в точке ξ, то в ней необходимо задать условия непрерывности:

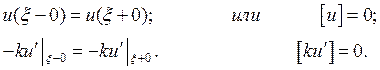
Воспользуемся стандартной разностной схемой для :

                                                              

Перепишем в виде:

                                          

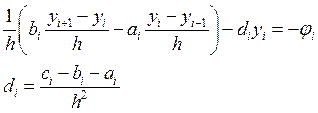
Разностная схема однородна, если ее коэффициенты во всех узлах сетки для любых коэффициентов ДУ вычисляются по одним и тем же формулам. Т.о. для однородной схемы удобно пользоваться безындексными обозначениями:

  

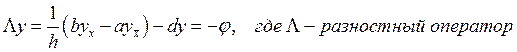
Определим погрешность аппроксимации : . V – произвольная достаточно гладкая функция. Если  имеют необходимое количество производных:

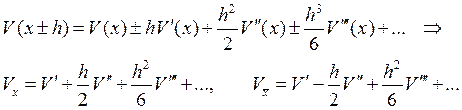
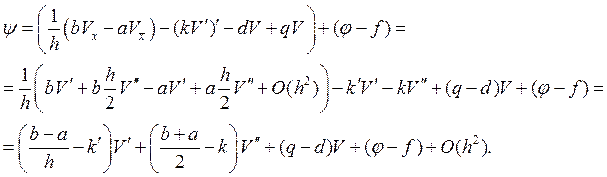
Т.о. схема будет иметь второй порядок аппроксимации, если:

Консервативные схемы

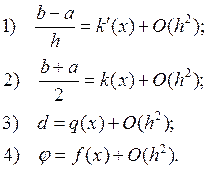
В основном ДУ выражают законы сохранения. Поэтому необходимо, чтобы и схемы отражали на сетке эти же законы сохранения! Такие схемы называются консервативными.

Проинтегрируем

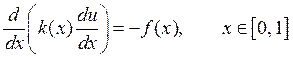                                                на : 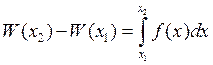. Тогда слева в равенстве стоит разность тепловых потоков на концах отрезка, а справа количество выделившегося/поглотившегося тепла.

Выпишем однородную схему для уравнения (3.1):

                                                   

                

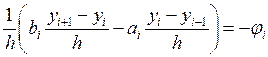
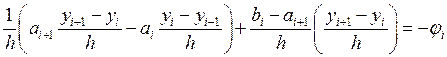
Просуммируем на :

                                                                

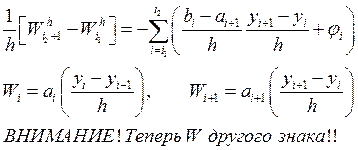
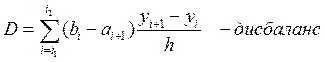
Величина D для произвольных разностных схем ≠0. Она обращается в ноль тогда и только тогда, когда                                                                                              

Это и есть необходимое и достаточное условие консервативности.

Методы баланса для построения консервативных схем

Дана задача: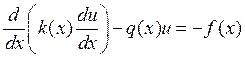                                                          

Для него закон сохранения (уравнение баланса, полученное с помощью интегрирования на [x₁,x₂]):

                                                        

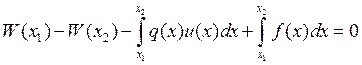
Тогда запишем уравнение баланса в полуцелых точках:

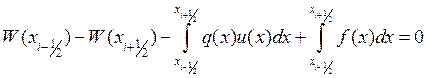                                            аппроксимируем кусочно-постоянной функцией: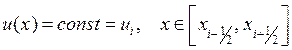

                                        

                                                

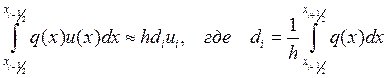
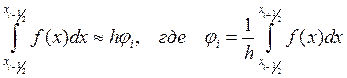
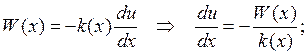
Проинтегрируем на отрезке:

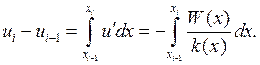
Будем считать, что на отрезке

                                                                                                    

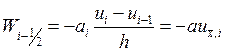
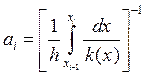
Подставим в формулы – и получим закон сохранения на сетке: