Будем аппроксимировать ![]() на конечном элементе
на конечном элементе ![]() с помощью функций
с помощью функций ![]() .
Для линейных конечных элементов с каждым конечным элементом ассоциировано 2
узла.
.
Для линейных конечных элементов с каждым конечным элементом ассоциировано 2
узла.
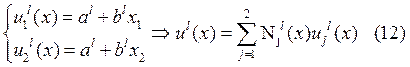 .
.
![]() -
интерполянтные кусочно-линейные базисные функции.
-
интерполянтные кусочно-линейные базисные функции.
3. Формулировка метода Ритца.
Пусть ![]() , т. е.
даны однородные краевые условия второго рода.
, т. е.
даны однородные краевые условия второго рода.
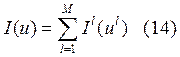 ,
, 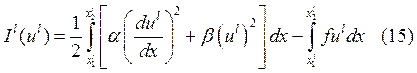 .
.
Подставим ![]() и
вычислим частные производные
и
вычислим частные производные 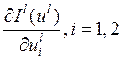 .
.
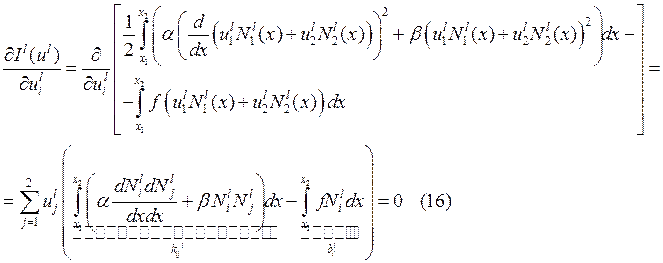
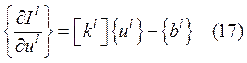
![]() ,
, ![]() - симметричная.
- симметричная.
Если ![]() или
могут быть аппроксимированы
или
могут быть аппроксимированы ![]() на конечном элементе, то
на конечном элементе, то
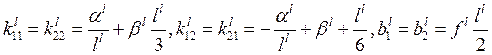
4. Ассемблирование (сборка) глобальной матрицы СЛАУ.
СЛАУ для определения решения ![]() может быть получена суммированием по всем
конечным элементам локальных матриц.
может быть получена суммированием по всем
конечным элементам локальных матриц.
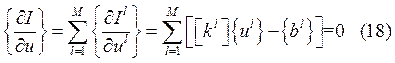
![]() -
соответствующие локальные матрицы и вектора.
-
соответствующие локальные матрицы и вектора.
![]() -
соответствующие локальные матрицы и вектора, дополненные до размера глобадьных.
-
соответствующие локальные матрицы и вектора, дополненные до размера глобадьных.
Пример:

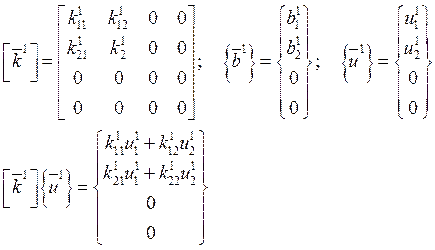
Аналогично:
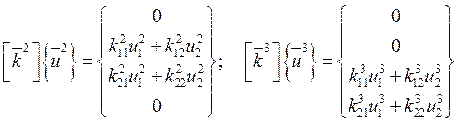
![]()
Аналогично для вектора правой части.
Учет краевых условий третьего рода.
Пусть в точке ![]() заданы краевые условия
третьего рода:
заданы краевые условия
третьего рода:
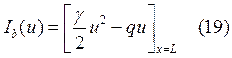 - добавка, которая позволяет
учесть третьи краевые условия. Дискретный аналог функционала
- добавка, которая позволяет
учесть третьи краевые условия. Дискретный аналог функционала ![]() имеет вид:
имеет вид:
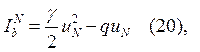 минимум его достигается, когда
минимум его достигается, когда 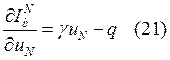
Аналогично соотношению ![]() определим
локальную матрицу для граничного элемента и рассмотрим вклад в данную матрицу
от функционала
определим
локальную матрицу для граничного элемента и рассмотрим вклад в данную матрицу
от функционала ![]() .
.
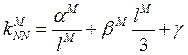 , где
, где ![]() - вклад
в соответствующую матрицу от краевого условия.
- вклад
в соответствующую матрицу от краевого условия.
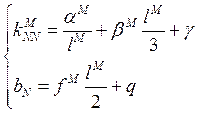 -
- ![]() - вклад
от краевого условия.
- вклад
от краевого условия.
Учет первых краевых условий.
На границе ![]() заданы краевые условия
Дирихле
заданы краевые условия
Дирихле ![]() .
.
Для того, чтобы от краевых условий второго рода перейти к
неоднородным условиям первого рода, надо в глобальной матрице заменить первую
строку на ![]() , а первую компоненту вектора правой части
на
, а первую компоненту вектора правой части
на ![]() .
.
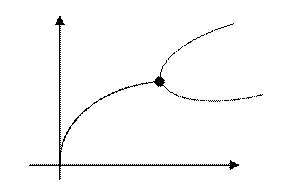 Бифуркация
означает раздвоение и употребляется для демонстрации всякой качественной
(топологической) перестройки картины при изменении параметров, от которых
зависит изучаемый процесс.
Бифуркация
означает раздвоение и употребляется для демонстрации всякой качественной
(топологической) перестройки картины при изменении параметров, от которых
зависит изучаемый процесс.
Самым простым примером бифуркаций является следующий рисунок, где жирной точкой отмечена точка бифуркации. Сам изучаемый объект может иметь различную природу. Это могут быть кривые на поверхности, функции или отображения, многообразия, векторные поля, дифференциальные или интегральные уравнения. Если объект зависит от некоторых параметров, то говорят, что задано семейство. Если мы интересуемся семейством локально (т.е. при малом изменении параметров в окрестности некоторых фиксированных значений), то говорят о деформации объекта, соответствующего этим значениям параметров.
Во многих случаях оказывается, что изучение всевозможных деформаций сводится к изучению одной, из которой получаются все остальные. Такая деформация (в некотором смысле – самая богатая) должна определять всевозможные бифуркации данного объекта. Такая деформация называется версальной.
Рассмотрим векторное поле, гладко зависящее от параметров. Пусть при некотором значении параметра поле имеет особую точку.
Теорема. Особая точка векторного поля, гладко зависящего от параметра, сама гладко зависит от параметра, пока все собственные числа линейной части поля в особой точке отличны от нуля.
Доказательство:
В окрестности изучаемой точки и изучаемого значения параметра семейство полей в
![]() -мерном фазовом пространстве задаётся
-мерном фазовом пространстве задаётся ![]() функциями от
функциями от ![]() переменной
(
переменной
(![]() переменных – координаты фазового
пространства, ещё одна переменная – параметр) вида
переменных – координаты фазового
пространства, ещё одна переменная – параметр) вида ![]() , где
, где ![]() .3
.3
Фазовое пространство – множество всевозможных состояний процесса.
По теореме о
неявной функции, эти уравнения локально определяют некоторую гладкую кривую ![]() при условии, что определитель матрицы
Якоби
при условии, что определитель матрицы
Якоби 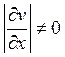 в соответствующей точке.
в соответствующей точке.
Имеем, что линейная часть поля есть матрица Якоби; соответственно, определитель этой матрицы будет равен произведению собственных значений линеаризованного поля в особой точке, а по предположению этот определитель отличен от нуля.
Замечание. Особые точки, в которых все собственные числа линеаризованного поля отличны от нуля, называются невырожденными.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.