получим: 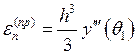 - локальная погрешность.
Локальная погрешность аппроксимации вычисляется на каждом шаге. Глобальная –
накапливается в течение всего процесса решения и имеет порядок
- локальная погрешность.
Локальная погрешность аппроксимации вычисляется на каждом шаге. Глобальная –
накапливается в течение всего процесса решения и имеет порядок ![]() на 1 меньше локальной.
на 1 меньше локальной.
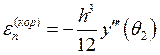 ,
, ![]() .
.
Разность погрешности между предсказанным и исправленным значением равна
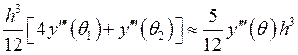
Обычно действуют так: предполагая, что ![]() на заданном отрезке не меняет знак (всегда
можно найти точку, для которой это выполняется), мы получаем, что
спрогнозированное и скорректированное значения лежат по разные стороны от
истинного значения
на заданном отрезке не меняет знак (всегда
можно найти точку, для которой это выполняется), мы получаем, что
спрогнозированное и скорректированное значения лежат по разные стороны от
истинного значения ![]() на данном шаге, а это дает
возможность оценки точности на каждом шаге, т. е. если погрешность велика, то
уменьшение шага в 2 раза даст уменьшение погрешности в 8 раз.
на данном шаге, а это дает
возможность оценки точности на каждом шаге, т. е. если погрешность велика, то
уменьшение шага в 2 раза даст уменьшение погрешности в 8 раз.
Пусть ![]() – аналитическое решение;
– аналитическое решение;
![]() – решение, вычисленное по формуле .
– решение, вычисленное по формуле . ![]() . Вычтем уравнения:
. Вычтем уравнения:
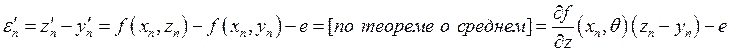 , где
, где ![]() .
Обозначим через
.
Обозначим через 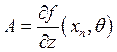 ,
, ![]() . Тогда
. Тогда ![]() . Получили разностное уравнение,
описывающее поведение погрешности. Применим этот аппарат к формуле . Подставим точное решение в неточную формулу и получим:
. Получили разностное уравнение,
описывающее поведение погрешности. Применим этот аппарат к формуле . Подставим точное решение в неточную формулу и получим:
![]()
Вычтем из формулу и воспользуемся
![]()
![]()
Устойчивость неоднородного уравнения определяется устойчивостью однородного уравнения . Решение будем искать в виде ![]() ,
тогда
,
тогда
![]() ,
,
![]()
Если ![]() , тогда
, тогда ![]() ; если
; если ![]() , тогда
, тогда ![]() . Т. о.
. Т. о. ![]() будет всегда
возрастать, т. е. метод простого прогноза неустойчив.
будет всегда
возрастать, т. е. метод простого прогноза неустойчив.
Проделав выкладки, аналогичные выкладкам для простого
прогноза получим характеристическое уравнение 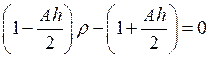 ,
решение которого:
,
решение которого:
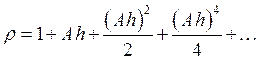
Соответственно, условие устойчивости будет 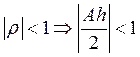 . Аналогичное условие можно получить, если
анализировать возмущенность многократного применения метода коррекции на первом
шаге вычислительного процесса:
. Аналогичное условие можно получить, если
анализировать возмущенность многократного применения метода коррекции на первом
шаге вычислительного процесса:
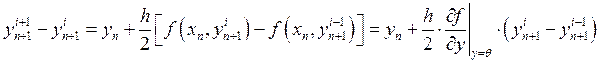 , где
, где 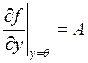
т. е. процесс будет сходиться
при 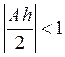 (то же самое условие), т. е. тогда, когда
(то же самое условие), т. е. тогда, когда ![]() - сжимающий оператор. Добиться
этого условия можно выбором шага
- сжимающий оператор. Добиться
этого условия можно выбором шага ![]() . Поэтому можно говорить
об устойчивости метода коррекции. Для выбранных нами ограничений
. Поэтому можно говорить
об устойчивости метода коррекции. Для выбранных нами ограничений ![]() прогноз неустойчив, а коррекция устойчива.
Выясним, как неустойчивость прогноза влияет на весь вычислительный процесс.
Формула описывает поведение
прогноз неустойчив, а коррекция устойчива.
Выясним, как неустойчивость прогноза влияет на весь вычислительный процесс.
Формула описывает поведение ![]() для коррекции.
для коррекции.
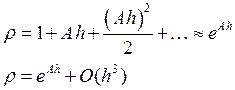
Рассмотрим модельное уравнение ![]() ,
, ![]() . Решение этого уравнения имеет вид
. Решение этого уравнения имеет вид ![]() , где
, где ![]() , а
значит это решение будет совпадать с формулой с точностью до
, а
значит это решение будет совпадать с формулой с точностью до ![]() .
.
Т. о. мы получили, что для
прогноза решение и погрешность ведут себя одинаково, т. е. мы предъявили
слишком жесткие требования к прогнозу, когда потребовали чтобы для устойчивости
![]() . Очевидно, что если решение возрастает как
геометрическая прогрессия, то погрешность, которая растет с такой же скоростью
или медленнее, не обязательно «испортит» решение, т.е. если решение строго
возрастающее, то факт, что погрешность также строго возрастает, не важен. Если
. Очевидно, что если решение возрастает как
геометрическая прогрессия, то погрешность, которая растет с такой же скоростью
или медленнее, не обязательно «испортит» решение, т.е. если решение строго
возрастающее, то факт, что погрешность также строго возрастает, не важен. Если ![]() и решение строго убывающее со скоростью
и решение строго убывающее со скоростью ![]() (
(![]() - номер
шага), то ясно, что если погрешность не убывает с такой скоростью, то она будет
преобладать в решении начиная с некоторого шага. И даже тот факт, что сама
погрешность ограниченна, в случае убывающего решения не помогает. Предыдущий
анализ позволяет сделать вывод, что от численного решения ДУ нужно требовать относительную
устойчивость, которая определяется как скорость роста погрешности по отношению
к росту решения. Если относительная устойчивость по модулю меньше 1
(относительная погрешность определяет относительную устойчивость), то
погрешность будет расти не быстрее решения.
- номер
шага), то ясно, что если погрешность не убывает с такой скоростью, то она будет
преобладать в решении начиная с некоторого шага. И даже тот факт, что сама
погрешность ограниченна, в случае убывающего решения не помогает. Предыдущий
анализ позволяет сделать вывод, что от численного решения ДУ нужно требовать относительную
устойчивость, которая определяется как скорость роста погрешности по отношению
к росту решения. Если относительная устойчивость по модулю меньше 1
(относительная погрешность определяет относительную устойчивость), то
погрешность будет расти не быстрее решения.
Если ![]() , то характеристические
корни уравнения прогноза будут иметь вид:
, то характеристические
корни уравнения прогноза будут иметь вид:
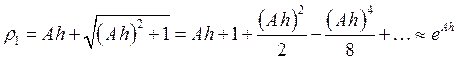 ;
; 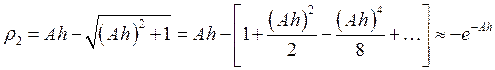
Если ![]() , то повторное
применение прогноза на одном и том же шаге дает разумные результаты; если
, то повторное
применение прогноза на одном и том же шаге дает разумные результаты; если ![]() , то
, то ![]() будет
увеличиваться по величине и колебаться по знаку, т. е. в данном случае прогноз
повторно лучше не применять.
будет
увеличиваться по величине и колебаться по знаку, т. е. в данном случае прогноз
повторно лучше не применять.
Методы прогноза и коррекции можно разделить на 2 класса:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.