Методы теории возмущений. Бифуркации., страница 13

Если , то в процессе решения допускается возрастание нормы разности , а это означает устойчивость сходимости.

Коэффициент в (4) можно выбрать независимо от классической константы Липшица для некоторого диапазона шагов , не зависящих от жесткости.

ВЫВОД:

Любой метод, предлагаемый для решения жестких задач, должен быть С-устойчив на классе F, чтобы иметь практическое применение. Например, методы Рунге-Кутты С-устойчивы на классе жестких задач, для которых классическая константа Липшица ограничена.

АБСОЛЮТНАЯ УСТОЙЧИВОСТЬ

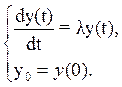(5)

- константа ( в общем случае комплексная)

Свяжем понятие абсолютной устойчивости с модельной скалярной задачей (5).

Любой метод Рунге-Кутты, заданный формулой (1), который применяется к уравнению (5), может быть записан в виде:

(6)

-некоторая функция

Обычно R - полином или рациональная функция с вещественными коэффициентами. Функция R называется ФУНКЦИЕЙ УСТОЙЧИВОСТИ МЕТОДА. Метод называется АБСОЛЮТНО УСТОЙЧИВЫМ для , если для этих z выполняется неравенство

Это неравенство выполняется для любой пары и , для которых .

Абсолютная устойчивость является естественным требованием в случае, когда .

Это означает что модуль точного решения есть всегда невозрастающая функция, т.е. на самом деле абсолютная устойчивость есть свойство контрактивности данного метода.

Множество всех точек z , для которых выполняется соотношение , называется ОБЛАСТЬЮ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ метода. Если область абсолютной устойчивости содержит левую полуплоскость, т.е. , то данный метод называется А-устойчивым. А-устойчивость означает безусловно-абсолютную устойчивость для уравнения (5), при условии что . Если метод А-устойчив, то и функция R называется А-устойчивой. Абсолютная устойчивость методов Рунге-Кутты полностью определяется свойствами функции устойчивости R.

Пусть дана система ДУ

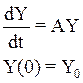(7)

А - матрица с постоянными коэффициентами

Тогда в общем виде метод Рунге –Кутты выглядит так:

(8)

где – некоторая функция от матрицы, которая тоже называется функцией устойчивости. Матричная функция существует, если комплекснозначная функция , определенная на спектре матрицы тоже существует.

Если – собственные значения матрицы /т.е. спектр/, то будут собственными значениями матрицы . Если А – нормальная матрица, то тоже будет нормальной матрицей. => Если А - нормальная матрица, то условия будут необходимыми и достаточными условиями контрактивности соответствующей нормы.

Разностные методы решения краевых задач для обыкновенных ДУ

Сеточная функция – функция дискретного аргумента . Множество сеточных функций образует конечномерное пространство. Т.к. сама сеточная функция зависит от h, как от параметра, поэтому обозначим семейство сеточных функций: H_h.

Введём понятие разностной аппроксимации оператора , т.е. заменим оператор в точке линейной комбинацией значений сеточной функции на некотором множестве узлов сетки – шаблоне .

Погрешность аппроксимации оператора L оператором L_h:

L_h имеет порядок аппроксимации m, если

Заменим краевую задачу: 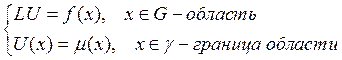ее дискретным аналогом: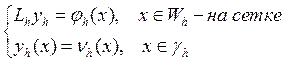

Функции зависят от шага сетки, т.е. меняя шаг сетки, получим семейства и соответственно семейство дискретных задач. Такое семейство задач называется разностной схемой.