1) система всегда имеет решение и при этом !.
2) элемент ![]() вида , где
вида , где ![]() – решение системы является элементом наилучшего приближения для элемента u в
– решение системы является элементом наилучшего приближения для элемента u в ![]() среди всех элементов подпространства
среди всех элементов подпространства ![]() .
.
Лемма: Ошибка обобщённого
метода Ритца ортогональна в ![]() подпространству
подпространству![]() .
.
Лемма: Последовательность
приближений ![]() , построенных по обобщённому методу Ритца
сходится к обобщённому решению операторного уравнения и определяет минимум
квадратичного функционала энергии .
, построенных по обобщённому методу Ритца
сходится к обобщённому решению операторного уравнения и определяет минимум
квадратичного функционала энергии .
Получим уравнение классического метода Ритца, выбрав в качестве квадратичного функционала – функционал энергии (8). Рассмотрим три случая:
При ![]() , тогда
с учетом вида решения
, тогда
с учетом вида решения 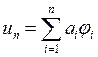 получим:
получим: 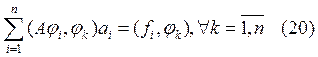 или формулу (20) можно переписать в виде
или формулу (20) можно переписать в виде ![]()
При ![]() , где
, где ![]() - оператор из линейной оболочки ГП, тогда
с учетом вида решения
- оператор из линейной оболочки ГП, тогда
с учетом вида решения 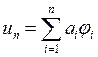 получим:
получим: 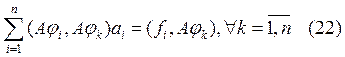 ,
или ее можно переписать в виде
,
или ее можно переписать в виде ![]()
При ![]() , где положительный
самосопряжённый оператор, тогда с учетом вида решения
, где положительный
самосопряжённый оператор, тогда с учетом вида решения 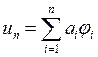 получим:
получим:
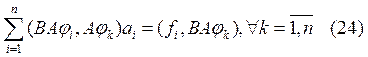 или формулу (24) можно переписать в виде
или формулу (24) можно переписать в виде ![]()
Для соотношений (20)-(25)
можно сказать, что различные модификации метода Ритца для определения
обобщённого решения операторного уравнения ![]() ,
отличаются друг от друга в рамках допускаемых предположений о задаче
минимизации функционала:
,
отличаются друг от друга в рамках допускаемых предположений о задаче
минимизации функционала:
-
выбором оператора ![]()
-
выбором координатных элементов, по которым приближённое решение ![]() .
.
Формулы (21), (23), (25)
демонстрируют, что невязка ![]() всегда будет
ортогональна некоторому конечномерному подпространству, которое определяется
следующим образом: в (21) это
всегда будет
ортогональна некоторому конечномерному подпространству, которое определяется
следующим образом: в (21) это ![]() , в (23) и (25) –
подпространство, которое является линейной оболочкой элементов
, в (23) и (25) –
подпространство, которое является линейной оболочкой элементов ![]() и
и ![]() соответственно.
Это свойство позволяет построить следующий формальный алгоритм построения
приближённого решения
соответственно.
Это свойство позволяет построить следующий формальный алгоритм построения
приближённого решения ![]() , при условии, что
, при условии, что ![]() и необязательно является симметричным.
и необязательно является симметричным.
Пусть, наряду с ![]() , определено некоторое подпространство,
построенное также, как и подпространство
, определено некоторое подпространство,
построенное также, как и подпространство ![]() , но по
другой системе векторов
, но по
другой системе векторов ![]() .
.
Подставим в ![]() элемент
элемент 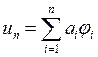 и
потребуем, чтобы невязка
и
потребуем, чтобы невязка ![]() была ортогональна
подпространству
была ортогональна
подпространству ![]() :
: 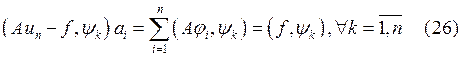 .
.
Метод, построенный таким образом, называется методом Галеркина, а система (26) называется системой уравнений метода Галеркина.
Пусть ![]() и
и ![]() -
- ![]() -мерные подпространства
-мерные подпространства ![]() , а
, а ![]() -
ортопроектор:
-
ортопроектор: ![]() . Тогда исходное операторное
уравнение можно заменить на
. Тогда исходное операторное
уравнение можно заменить на
![]() . (27)
. (27)
Уравнение (27) – уравнение проекционного метода. Из уравнений (26) и (27) следует, что метод Галеркина – проекционный метод.
При решении соответствующих
задач чаще всего используют вариационно-разностные, проекционно – разностные
методы, МКЭ. Специфика данных методов заключается в том, что их координатными
элементами являются финитные функции, которые построены специальным образом.
Матрица СЛАУ – разреженная. Для того, чтобы при увеличении размерности ![]() , получить устойчивое решение, необходимо
потребовать не ухудшения числа обусловленности при увеличении
, получить устойчивое решение, необходимо
потребовать не ухудшения числа обусловленности при увеличении ![]() .
.
Пусть дана краевая задача:
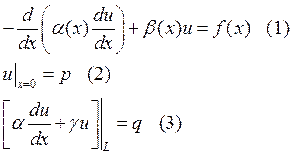
Если ![]() -
разрывная функция, то будем считать, что для решения и для потока выполняются
условия сопряжения:
-
разрывная функция, то будем считать, что для решения и для потока выполняются
условия сопряжения:
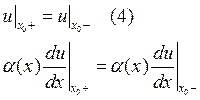 (5)
(5)
1. Вариационная постановка.
![]() - самосопряжённый положительно определённый
оператор. Решение задачи (1)-(5) доставляет минимум функционалу:
- самосопряжённый положительно определённый
оператор. Решение задачи (1)-(5) доставляет минимум функционалу: 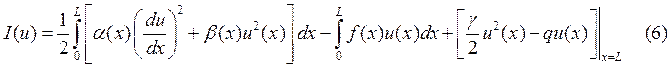
и удовлетворяет главным краевым условиям (2).
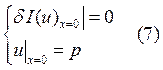
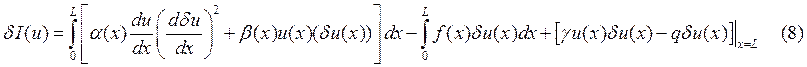
![]() -
непрерывная функция в области
-
непрерывная функция в области ![]() .
.
Проинтегрируем по частям вариацию (8):
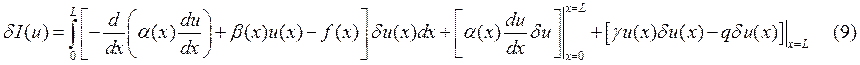
Так как ![]() ,
,
![]() , то:
, то:
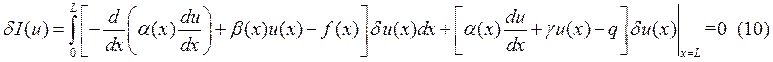 , где (10) – функционал (9) с
учетом главного краевого условия.
, где (10) – функционал (9) с
учетом главного краевого условия.
![]() , если
выполняется (1), (3).
, если
выполняется (1), (3).
Если ![]() -
разрывна и выполнены условия сопряжения (4) и (5), то эти условия естественным
образом учитываются в функционале (6). Так как
-
разрывна и выполнены условия сопряжения (4) и (5), то эти условия естественным
образом учитываются в функционале (6). Так как ![]() -
предполагается непрерывным, то
-
предполагается непрерывным, то ![]() - тоже предполагается
непрерывной. Данные условия идеального контакта (4), (5) дополнительного учета
в функционале (6) не требуют.
- тоже предполагается
непрерывной. Данные условия идеального контакта (4), (5) дополнительного учета
в функционале (6) не требуют.
2. Дискретизация и интерполяция.
-построение сетки
![]()

Введем локальную нумерацию в
конечном элементе: ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.