В реализации физических задач, математическая модель которых
выписывается в виде обыкновенных ДУ, правые части этих обыкновенных ДУ могут
содержать параметры. Значения этих параметров обычно определяются приближенно.
Возникает вопрос об изменении решения при малом изменении этих параметров. Если
вопрос зависимости решения от малого изменения параметра от задачи Коши решается
на неограниченном промежутке ![]() , то эта задача решается
методами теории устойчивости.
, то эта задача решается
методами теории устойчивости.
Пусть данa задача:
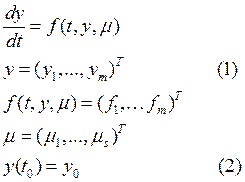
где ![]() - это вектор неизвестных
параметров.
- это вектор неизвестных
параметров.
Рассмотрим скалярное уравнение:
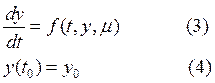
Пусть функция ![]() определена в области
определена в области ![]() :
:
![]()
Пусть также ![]() непрерывна в
непрерывна в ![]() по совокупности аргументов и удовлетворяет
условию Липшица по
по совокупности аргументов и удовлетворяет
условию Липшица по ![]() , т.е.
, т.е.
![]()
Здесь ![]() - одна и та же константа
для всех
- одна и та же константа
для всех ![]() .
.
При фиксированном ![]() на отрезке
на отрезке ![]() , где
, где  , где
, где ![]() .
.
На этом отрезке, по Т. о ![]() и
и ![]() , определена интегральная кривая – решение
(3), (4). Меняя
, определена интегральная кривая – решение
(3), (4). Меняя ![]() , в силу независимости констант
, в силу независимости констант ![]() и
и ![]() от
от ![]() , мы получаем семейство интегральных кривых
, мы получаем семейство интегральных кривых
![]() на
на ![]() .
.
Теорема 1
Пусть ![]() определена и непрерывна
в области
определена и непрерывна
в области ![]() и удовлетворяет условию Липшица (5). Тогда
решение задачи (3), (4)
и удовлетворяет условию Липшица (5). Тогда
решение задачи (3), (4) ![]() на
на ![]() непрерывно по
непрерывно по ![]() для всех
для всех
![]() .
.
В задаче (3), (4) будем считать ![]() , т.е.
исследуем поведение задачи в окрестности нуля. Если же
, т.е.
исследуем поведение задачи в окрестности нуля. Если же ![]() ,
то заменой
,
то заменой ![]() можно перейти к рассматриваемому случаю.
можно перейти к рассматриваемому случаю.
2. Регулярные возмущения.
Задача вида (3), (4) называется РЕГУЛЯРНО ВОЗМУЩЕННОЙ
(параметры ![]() находятся в правой части уравнения). На
основе теоремы 1 построим приближенное решение (3), (4). Пусть в (3), (4)
находятся в правой части уравнения). На
основе теоремы 1 построим приближенное решение (3), (4). Пусть в (3), (4) ![]() :
:
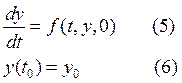
Пусть ![]() - решение (5), (6). Из
теоремы 1 имеем:
- решение (5), (6). Из
теоремы 1 имеем:
на отрезке ![]()
![]()
причем ![]() при
при ![]() .
.
Таким образом, ![]() - приближенное решение
(3), (4);
- приближенное решение
(3), (4); ![]() - погрешность приближенного решения и асимптотическая
формула (7) позволяет достаточно хорошо описать
- погрешность приближенного решения и асимптотическая
формула (7) позволяет достаточно хорошо описать ![]() с
помощью
с
помощью ![]() при
при ![]() .
.
Теорема 2.
Пусть в некоторой области ![]() функция
функция
![]() обладает непрерывными и равномерно
ограниченными частными производными по
обладает непрерывными и равномерно
ограниченными частными производными по ![]() и
и ![]() до порядка
до порядка ![]() включительно.
Тогда существует отрезок
включительно.
Тогда существует отрезок ![]() , на котором для решения
(3)
, на котором для решения
(3) ![]() справедливо соотношение (7):
справедливо соотношение (7):
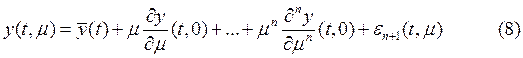 , причем
, причем ![]() при
при
![]() и
и ![]() .
.
Доказательство:
Соотношение (8) получается следующим образом: представим ![]() в виде ряда по степеням
в виде ряда по степеням ![]() . В результате будем иметь:
. В результате будем иметь:
![]()
Подставляя (9) в (3), при этом воспользуемся тем, что правая
часть уравнения имеет частные производные по ![]() и
и ![]() вплоть до
вплоть до ![]() порядка,
получаем (разложили правую часть в ряд Тейлора):
порядка,
получаем (разложили правую часть в ряд Тейлора):
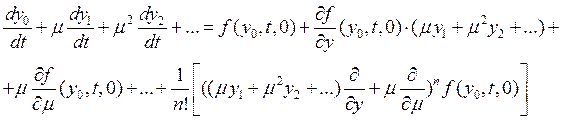
Подставим (9) в начальное условие (4). Пусть ![]() . Тогда
. Тогда
![]()
В последних двух соотношениях приравняем коэффициенты при
одинаковых степенях ![]() . Получили бесконечную систему ДУ
с начальными условиями:
. Получили бесконечную систему ДУ
с начальными условиями:
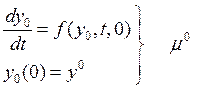
Это соответствует начальным условиям (5), (6) и значит ![]() . Далее
. Далее
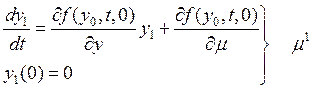
Последовательно решая эти задачи, определим (9) –
асимптотический ряд или разложения по малому параметру ![]() для
решения
для
решения ![]() по степеням
по степеням ![]() .
.
Теорема доказана.
Пример.
 (внимание: вероятно нужно сделать замену
(внимание: вероятно нужно сделать замену ![]() )
)
Будем искать решение в виде разложения (9). Определим первые три члена разложения.
![]()
После подстановки в исходное уравнение будем иметь:
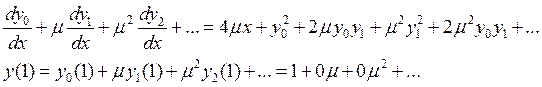
Приравняем коэффициенты при одинаковых степенях ![]() :
:
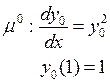

Решив эти уравнения, мы найдем интересующие нас члены разложения (9).
3. Сингулярные возмущения.
В различных приложениях достаточно часто встречаются задачи, к которым теория регулярных возмущений не применима.
Пусть дана задача:

Положим ![]() . Получаем уравнение
более низкого порядка и для решения нам понадобится одно начальное условие. Мы
не можем учесть все факторы, определяемые (1). И вблизи точки
. Получаем уравнение
более низкого порядка и для решения нам понадобится одно начальное условие. Мы
не можем учесть все факторы, определяемые (1). И вблизи точки ![]() мы не получим нужного решения уравнения
(1). Сделаем замену переменных:
мы не получим нужного решения уравнения
(1). Сделаем замену переменных:
![]()
Тогда
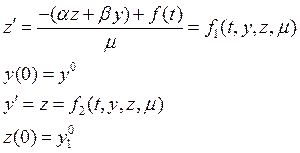
Если эти условия удовлетворяют теореме 2, то решение можно
искать в виде асимптотического разложения. Для функции ![]() условия
теоремы 2 нарушаются, так как эта функция терпит разрыв при
условия
теоремы 2 нарушаются, так как эта функция терпит разрыв при ![]() .
.
Рассмотрим задачу:
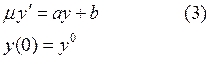
Решением этой задачи является:
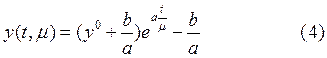
Пусть в (3) ![]() , тогда
, тогда ![]() и
и 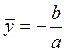
Исследуя (3), мы получим, что (4) близко к ![]() при выполнении ряда специальных условий:
при выполнении ряда специальных условий:
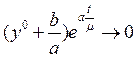
Рассмотрим решение (3) в ![]() . Тогда
. Тогда ![]() , если
, если
![]() при
при ![]()
![]() при
при ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.