Разностная схема – система
алгебраических уравнений. Решения ![]() и
и ![]() - величины разной природы. Схема, которую
будем строить должна сохранять все внутренние свойства исходной задачи.
- величины разной природы. Схема, которую
будем строить должна сохранять все внутренние свойства исходной задачи.
Сеточная функция ![]() и решение дифференциального уравнения -
и решение дифференциального уравнения - ![]() удовлетворяют уравнениям разной природы,
поэтому для оценки близости решения разностной задачи (4) к решению непрерывной
задачи (3) используем кроме сходимости ещё два понятия: аппроксимации и
устойчивости разностной схемы.
удовлетворяют уравнениям разной природы,
поэтому для оценки близости решения разностной задачи (4) к решению непрерывной
задачи (3) используем кроме сходимости ещё два понятия: аппроксимации и
устойчивости разностной схемы.
Будем говорить, что разностная схема имеет ![]() порядок аппроксимации на решении
задачи (3), если
порядок аппроксимации на решении
задачи (3), если ![]() такое
такое ![]() ,
что
,
что ![]() выполняется оценка:
выполняется оценка:
![]() , (7)
, (7)
где ![]() и
и ![]() -
константы, не зависящие от
-
константы, не зависящие от ![]() .
.
Схема называется устойчивой по начальным
условиям и правой части уравнения (5), если ![]() такое
такое ![]() , что
, что ![]() :
:
![]() , (8)
, (8)
где ![]() ,
, ![]() -
возмущение правой части и решения. Таким образом, малое изменение исходных
данных соответствует малому изменению решения.
-
возмущение правой части и решения. Таким образом, малое изменение исходных
данных соответствует малому изменению решения.
Теорема
Если разностная схема (4) устойчива и аппроксимирует задачу
(3) с порядком ![]() , то решение
, то решение ![]() при
при ![]() сходится
к решению (3), т.е.
сходится
к решению (3), т.е. ![]() , причём порядок сходимости равен
, причём порядок сходимости равен
![]() , т.е. имеет место (6).
, т.е. имеет место (6).
Доказательство.
Пусть ![]() , тогда по определению
порядка аппроксимации:
, тогда по определению
порядка аппроксимации:
![]() .
.
![]() , здесь для
, здесь для ![]() имеет место оценка
имеет место оценка ![]() (из (7) следует
(из (7) следует ![]() ),
а т.к.
),
а т.к. ![]() - решение возмущённой разностной задачи
(схемы) и эта схема устойчива, то получим:
- решение возмущённой разностной задачи
(схемы) и эта схема устойчива, то получим:
![]() [следует из устойчивости
(из (8))]
[следует из устойчивости
(из (8))] ![]() .
.
1.Пусть
дано уравнение (1), (2). Выясним, как получить разностную схему. Выпишем для
функции ![]() разложение в ряд Тейлора в окрестности
точки
разложение в ряд Тейлора в окрестности
точки ![]() :
:
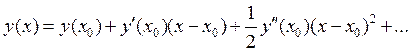
Если хотим ограничиться одним членом разложения, то
![]() ,
,
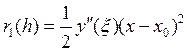 ,
, ![]() .
.
Если ![]() , получим
, получим ![]() ,
,
![]() (3).
(3).
Формула (3) – явный метод Эйлера.
В общем виде: ![]() ,
, ![]()
Остаточный член ![]() характеризует локальную
ошибку метода Эйлера, т.е. ошибку на каждом шаге. За
характеризует локальную
ошибку метода Эйлера, т.е. ошибку на каждом шаге. За ![]() шагов
работы метода образуется глобальная ошибка.
шагов
работы метода образуется глобальная ошибка.
Замечание. Порядок глобальной ошибки, относительно
шага ![]() , на единицу меньше, чем порядок локальной
ошибки, а именно порядок глобальной ошибки определяет (аппроксимирует) порядок
соответствующего разностного уравнения и точного решения задачи Коши. Таким
образом, локальная ошибка для метода Эйлера
, на единицу меньше, чем порядок локальной
ошибки, а именно порядок глобальной ошибки определяет (аппроксимирует) порядок
соответствующего разностного уравнения и точного решения задачи Коши. Таким
образом, локальная ошибка для метода Эйлера ![]() ,
порядок глобальной -
,
порядок глобальной - ![]()
![]() метод
Эйлера относится к методам первого порядка.
метод
Эйлера относится к методам первого порядка.
2. Для полученной схемы Эйлера рассмотрим разностную аппроксимациюпервой производной.
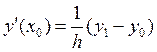 - значение производной в точке
- значение производной в точке ![]() подставим в формулу (3), получим
разностную схему.
подставим в формулу (3), получим
разностную схему.
3. Квадратурный способ
В соответствии с теоремой о существовании и единственности исходное дифференциальное уравнение может быть записано в эквивалентной интегральной постановке:
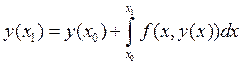 (4).
(4).
Построим аппроксимацию для (4), т.е.интеграл 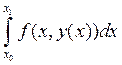 заменим
некоторыми квадратурными формулами.
заменим
некоторыми квадратурными формулами.
Если воспользуемся формулой прямоугольника, с вычисленными значениями в левой точке, то получим соотношение (3).
1. Если в (4) воспользоваться формулой прямоугольника, определённой по правой точке отрезка, то получим следующую модификацию:
(5) ![]() - неявный метод Эйлера (тоже имеет
первый порядок).
- неявный метод Эйлера (тоже имеет
первый порядок).
Повысить порядок метода можно, если рассмотреть линейную комбинацию методов (3) и (5):
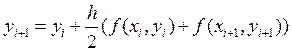 - метод трапеций.
- метод трапеций.
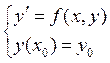
Пусть дана задача Коши и пусть правая часть имеет непрерывные частные производные вплоть до ![]() -го порядка. Тогда решение будет иметь
непрерывные производные вплоть до порядка
-го порядка. Тогда решение будет иметь
непрерывные производные вплоть до порядка ![]() .
Рассмотрим:
.
Рассмотрим:
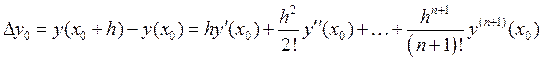
Все производные в формуле можно вычислить используя :
![]() где
где ![]() -
постоянные коэффициенты;
-
постоянные коэффициенты; ![]() ;
; ![]() - коэффициенты,
- коэффициенты, ![]() -
шаг дискретизации.
-
шаг дискретизации.
Выбрав шаг ![]() , зная коэффициенты
, зная коэффициенты ![]() ,
,![]() , можно определить решение
, можно определить решение ![]() в различных точках. Выбор коэффициентов
в различных точках. Выбор коэффициентов ![]() ,
,![]() , производится таким
образом, чтобы разложения и совпадали до возможно более высоких степеней
, производится таким
образом, чтобы разложения и совпадали до возможно более высоких степеней ![]() . Этим условиям удовлетворяет
. Этим условиям удовлетворяет
метод Рунге-Кутты второго порядка
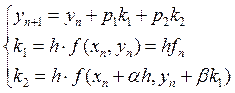
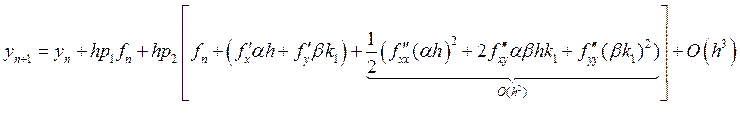
![]() (из
формулы (3))
(из
формулы (3))
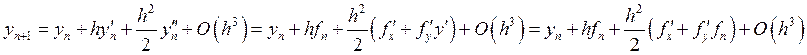
(из формулы (2))
![]() ;
; 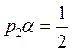 ;
; 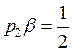 .
.
Параметром выбираем ![]() . Выберем
. Выберем 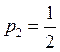 ,
получим
,
получим 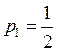 ;
; ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.