Методы теории возмущений. Бифуркации., страница 16

Симметричные билинейные формы и построение энергетических пространств.

Пусть  – всюду плотное в  гильбертовом пространстве  множество и на элементах этого множества  определена симметричная билинейная форма . Это означает, что любой паре  поставлено в соответствие некоторое число , обладающее следующими свойствами:

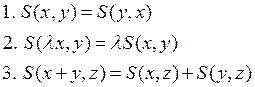
Квадратичной формой билинейной формы  называется форма .

Билинейная форма  S(x,y) называется положительно определенной, если            (2)

Замечание 1

Билинейную форму при  выполнении условия (2) можно интерпретировать как скалярное произведение на множестве , т.е.

                                            (3)

тогда норма, порождаемая этим скалярным произведением принимает вид:

       (4)

Замечание 2

Согласно (2)  в пространстве  будет подчинена норме  на множестве .

Если множество  совпадает со всем пространством , то билинейная форма  будет называться эрмитовой, а множество  будет гильбертовым пространством с новым скалярным произведением.

Пусть билинейная форма положительно определена и множество  не совпадает с . Определим новое гильбертово пространство  следующим образом: введем на множестве  скалярное произведение (3) и норму (4). Затем пополним множество  в новой норме (4). В результате этой операции получим новое гильбертово пространство , которое называется энергетическим.

Остов этого пространства, т.е. всюду плотная часть, состоит из элементов  из гильбертова пространства , в него добавлены некоторые предельные элементы из , поскольку, благодаря неравенству (2), любая фундаментальная последовательность в норме (4) остается фундаментальной и в норме исходного пространства .

Задача о наилучшем приближении. Ортогональные разложения в Гильбертовом пространстве

В Гильбертовом пространстве H вследствие его полноты, своеобразия метрики и наличия понятия ортогональности для достаточно широко класса множеств   возможность решения задачи о наилучшем приближении элементов  элементами  ( называется аппроксимирующим множеством).

Теорема. Решение задачи  для связного замкнутого множества   и !.

Следствие.  .

Теорема Рисса. ограниченного функционала , определённого всюду на

 // - действие функционала

Теорема Хана-Банаха. Пусть  – замкнутое подпространство Банахова пространства . Если  –линейный функционал, определённый на , то  линейный непрерывный функционал g, определённый на , и являющийся расширением   с той же нормой.

Самосопряжённый оператор  – ограниченный симметричный оператор, для которого область определения – всё . Если   - самосопряженный, то имеет место  

Самосопряжённый оператор – частный случай симметричного ограниченного оператора. В общем случае симметричный оператор не ограничен.

Квадратичные функционалы с положительно определённым симметричным оператором и обобщённые решения операторных уравнений

 – вещественное Гильбертово пространство.  – симметричный положительно определённый оператор.  – линейный ограниченный функционал. Область определения : . . Рассмотрим квадратичную форму           

                             

Исследуем задачу поиска inf этого функционала и , если последний . Поскольку оператор  может быть определён не на всех x из H, то построим новое энергетическое пространство  и на элементах  определим новое скалярное произведение. Пусть . Пополним множество  по норме   и получим новое пространство  со скалярным произведением . Вследствие того, что оператор  положительно определённый

 Т.е. эти две нормы подчинены, а значит  будет состоять из элементов пространства H и при этом всегда будут выполняться следующие соотношения: линейный функционал , ограниченный на , будет ограничен и на  : . По теореме Рисса  и в этом случае квадратичный функционал примет вид:

                   

Если , то .  достигает наименьшее значение  при .

Квадратичный функционал  - функционал ошибок, его минимум равен нулю при

Основные типы функционалов, используемые при решении операторного уравнения Au=f