Применим второе уравнение из системы (5) в виде:
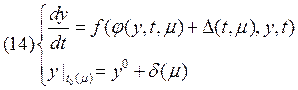
Согласно первому пункту теоремы,
величины ![]() и
и ![]() будут
сколь угодно малыми при малом
будут
сколь угодно малыми при малом ![]() . Соответственно,
. Соответственно, ![]() тоже будет сколь угодно малым при
достаточно малом
тоже будет сколь угодно малым при
достаточно малом ![]() и при
и при ![]() из
окрестности
из
окрестности ![]() .
.
3.
Покажем, что при неравенство (13) выполняется ![]() и
не существует такой точки
и
не существует такой точки ![]() , для которой это
неравенство обращается в равенство. Предположим противное. Пусть при
, для которой это
неравенство обращается в равенство. Предположим противное. Пусть при ![]() выполняется равенство
выполняется равенство ![]() , и рассмотрим вспомогательную функцию
, и рассмотрим вспомогательную функцию ![]() . В силу предположения вычислим
. В силу предположения вычислим ![]() .
.
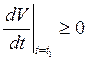 .
.
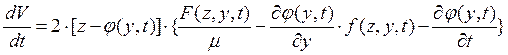 .
.
Поскольку правая часть ![]() , то это значит, что знак выражения в
фигурных скобках при достаточно малых
, то это значит, что знак выражения в
фигурных скобках при достаточно малых ![]() определяются
знаком
определяются
знаком ![]() , и, следовательно, в силу малости
, и, следовательно, в силу малости ![]() знаком выражения
знаком выражения 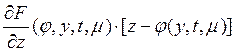 .
Т.е. знак всего выражения
.
Т.е. знак всего выражения ![]() будет определятся
знаком функции
будет определятся
знаком функции  , а из условий 3)-4) теоремы
следует, что
, а из условий 3)-4) теоремы
следует, что  (устойчивый корень), а значит,
(устойчивый корень), а значит, 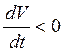 . Полученное противоречие и доказывает
теорему.◄
. Полученное противоречие и доказывает
теорему.◄
Замечание: из доказательства теоремы следует, что предельный
переход ![]() будет равномерным на этом отрезке, а
предельный переход
будет равномерным на этом отрезке, а
предельный переход ![]() нет.
нет.
В окрестности точки ![]() существует
область, в которой
существует
область, в которой ![]() - компонента решения задачи
(5)-(6) сильно отличается от
- компонента решения задачи
(5)-(6) сильно отличается от ![]() - компоненты
вырожденной задачи, т.е. от устойчивого корня
- компоненты
вырожденной задачи, т.е. от устойчивого корня ![]() . Такая
область называется пограничным слоем. На основе теоремы Тихонова можно выписать
следующее асимптотическое представление для задачи (5)-(6)
. Такая
область называется пограничным слоем. На основе теоремы Тихонова можно выписать
следующее асимптотическое представление для задачи (5)-(6)
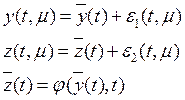
Данные асимптотического разложения будут кроме степенных
(регулярных) членов содержать некоторые функции (пограничные члены), зависящие
от ![]() нестепенным образом. Эти члены ряда,
отличные от нуля, в окрестности точки
нестепенным образом. Эти члены ряда,
отличные от нуля, в окрестности точки ![]() и с
ростом
и с
ростом ![]() быстро убывают.
быстро убывают.
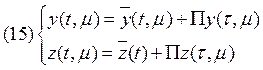
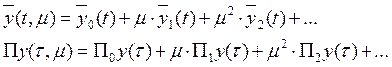
Рассмотрим как ряд со степенями ![]() , но с
коэффициентами, зависящими от
, но с
коэффициентами, зависящими от ![]() .
.
Сделав в (5) замену 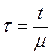 ,
получим систему (9), а теперь подставим (9) в (5), при этом умножив на
,
получим систему (9), а теперь подставим (9) в (5), при этом умножив на ![]() .
.
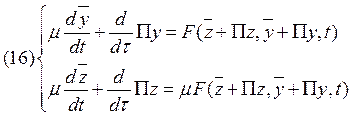
Правую часть системы (16) представим в виде:
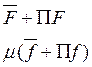
Получаем бесконечную систему ДУ, приравняв в системе (16)
коэффициенты при одинаковых степенях ![]() , причем отдельно для
регулярного и сингулярного ряда.
, причем отдельно для
регулярного и сингулярного ряда.
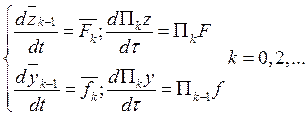
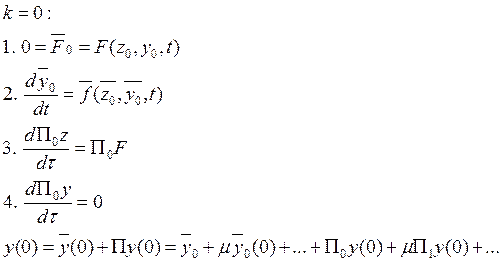
Аналогично для ![]() .
.
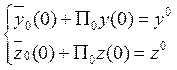
Решением первого уравнения является ![]() -
устойчивый корень. Решением последнего будет
-
устойчивый корень. Решением последнего будет ![]() . Но нам
известно, что при
. Но нам
известно, что при ![]()
![]() .
.
Получаем, что
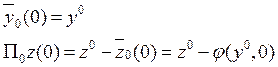
Начальные условия получены. Для ![]() решаем
аналогично.
решаем
аналогично.
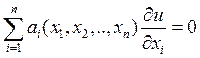 (1)
(1)
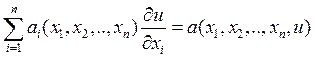 (2)
(2)
(1) – уравнение в ч.п. первого порядка
(2) – квазилинейное уравнение
Линейные уравнения первого порядка
Пусть ![]() икоэффициенты
уравнения (1)
икоэффициенты
уравнения (1) ![]() не обращаются в ноль
одновременно в любой точке области G.
не обращаются в ноль
одновременно в любой точке области G.
Решением уравнения (1) будем называть любую функцию, которая
имеет частные производные по всем переменным ![]() и
которая обращает уравнение (1) в тождество.
и
которая обращает уравнение (1) в тождество.
Геометрически решение задачи (1) можно интерпретировать как
поверхность в пространстве ![]() и которая называется интегральной
поверхностью.
и которая называется интегральной
поверхностью.
Рассмотрим двумерную задачу
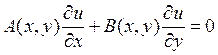 (3)
(3)
Выражение в левой части можно интерпретировать как скалярное
произведение некоторого векторного поля (A(x,y),B(x,y)) и grad u(x,y). Таким образом, (3) означает, что производная u по направлению вектора ![]() равна 0.
Обозначим через
равна 0.
Обозначим через ![]() -кривую на плоскости xy, которая обладает следующими свойством: касательный вектор
этой кривой коллинеарен вектору
-кривую на плоскости xy, которая обладает следующими свойством: касательный вектор
этой кривой коллинеарен вектору![]() .
.
Тогда параметрическое представление кривой ![]() будет иметь вид:
будет иметь вид:
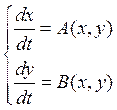 (4)
(4)
Фазовые траектории системы (4), которые называются интегральными кривыми, можно записать в виде
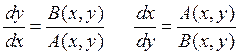 (5)
(5)
эти уравнения называются характеристиками дифференциального уравнения в частных производных (3). Обычно они записываются в форме
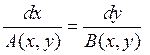 (6)
(6)
В силу того, что ![]() , через каждую точку
области G проходит одна и только одна характеристика.
Пусть u(x,y)-
решение (3) или интегральная поверхность (3).
, через каждую точку
области G проходит одна и только одна характеристика.
Пусть u(x,y)-
решение (3) или интегральная поверхность (3).
u(x,y)=u(x(t),y(t))
Значит, производная 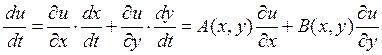 получим,
что
получим,
что 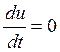 (из (3)), значит u
от t не зависит, т.е. характеристика является линией
уровня интегральной поверхности.
(из (3)), значит u
от t не зависит, т.е. характеристика является линией
уровня интегральной поверхности.
Рассмотрим кривую ![]() , не совпадающую с
характеристикой.
, не совпадающую с
характеристикой.
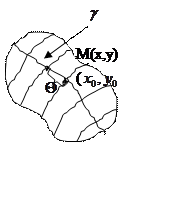 Через каждую точку области можно провести характеристику.
Через каждую точку области можно провести характеристику.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.