Методы теории возмущений. Бифуркации., страница 11

1)  Методы типа Милна – включают дополнительно несколько старых значений функции (например , )

2)  Методы типа Адамса-Башфорта – включают дополнительно несколько старых значений производных (например , ).

Преимущества метода прогноза и коррекции

1.  Разность между прогнозируемым и скорректированным значениями дает оценку ошибок на каждом шаге вычислительного процесса и, следовательно, может быть использована для контроля величины шага интегрирования.

2.  По сравнению с методами Рунге-Кутты на каждом шаге вычислительного процесса производная вычисляется реже (один или два раза, для Р-К два-четыре раза).

Основные минусы методов прогноза и коррекции:

1.  Неустойчивость.

2.  Методы прогноза-коррекции  не «самоначинающиеся» в отличие от методов Рунге-Кутты.

Численное решение задачи Коши для жестких систем ОДУ

Сущность явления жесткости состоит в следующем. Решение, которое нужно вычислить, меняется медленно, однако у него существуют быстро затухающие возмущения. Наличие быстро затухающих возмущений затрудняет получение медленно меняющегося решения численным методом. Жесткость имеет место тогда, когда искомое решение носит гладкий характер (т.е. медленно меняется) в то время как малые возмущения, которые порождаются погрешностями вычислений, быстро затухают.

При построении дискретного аналога для жестких задач нужно учитывать, что Ч.М. должен подавить эти возмущения так же, как это происходит в дифф. задаче.

ПРИМЕР

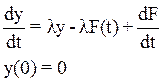   (1)

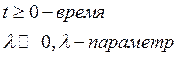
F(t)-  медленно меняющаяся гладкая функция

Аналитическое решение  имеет вид:

На следующем шаге

- малая величина

      (2)

По условию  (большое отрицательное число) =>После очень небольшого прошествия времени жесткая компонента решения  в решении уже почти не присутствует. =>Независимо от начального значения  в численном решении на большей части отрезка интегрирования [0,T]  преобладает медленно меняющаяся компонента решения. (В данном случае функция F(t)) Из (2) следует, что существование в любой момент времени t возмущения медленно меняющейся компоненты F(t) с ростом t практически отсутствует. => Задача (1) - очень устойчивая (по Ляпунову): т.е. малые возмущения исходных данных должны приводить к малому изменению решения.

Рассмотрим два метода численного решения задачи (1)

1. МЕТОД ЭЙЛЕРА

Воспользуемся схемами Рунге-Кутты 1-ого порядка.

                       (3)

                  (4)

Сравним, полученный по формулам (3) и (4) с аналитическим решением.

   (2’)

Подставляя правую чатсь формулы (1) в формулу (3) получим: решение уравнения

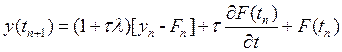  (3’)

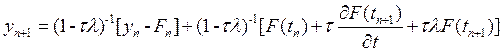      (4’)

Разность между  и  можно интерпретировать как возмущение гладкого решения F(t) в момент времени  .

В аналитическом решении это возмущение быстро убывает, т.к. умножено на , а  /формула(2’)/

В формулах (3’) и (4’) разность   и  можно интерпретировать аналогично => Ч.М. должен быть в состоянии подавить эту разность для значений  , причем шаг  определяется только в зависимости от поведения функций F(t) /это идеальное поведение/. В формуле (3’) разность  будет подавляться только в случае (*) Т.о. получаем условие численной устойчивости метода (3’), который накладывает серьезные ограничения на выбор шага . Если  и F(t) – очень гладкая функция, то в этом случае аппроксимацию для :

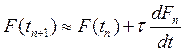
можно считать приемлемой, а это соотношение выполняется для , которое значительно больше, чем из ограничения (*).

Поскольку (3’) - явный метод, исходные ограничения на  можно смягчить, т.к. оценка на  завышена. Это можно сделать если F(t) – гладкая. Т.о. более крупный шаг  даёт хорошее решение.

Сильная устойчивость ДУ оказывается недостатком с точки зрения распространения погрешности численного решения при применении классических явных методов.

Рассмотрим формулу (4’). Разность   быстро убывает и оказывается, что для любого фиксированного шага  , т.е. неявный метод вполне удовлетворительно подходит для решения задачи (1).

ВЫВОД: