Методы теории возмущений. Бифуркации., страница 5

Точка пересечения характеристики с кривой  будет однозначно определять эту характеристику, т.е. образует однопараметрическое семейство, в качестве параметра можно выбрать расстояние  по кривой  от каждой фиксированной точки .

Положение точки М на каждой характеристике определяется значением параметра t, который описывает саму характеристику. Поэтому из (4) можно значение t определить с точностью до произвольной постоянной.

Будем считать, что точка пересечения каждой характеристики с кривой  соответствует значению параметра . Таким образом, в области G каждой точке M(x,y) можно поставить в соответствие пару чисел , где -определяет характеристику, проходящую через точку M, а t- значение параметра на характеристике, отвечающее точке М.

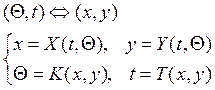            (8)

В новых переменных  и t  уравнение характеристики имеет вид:

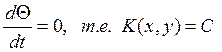          (9)

Теперь можно рассматривать u, как функцию параметра и t:

В силу соотношения  (8), уравнение (3) в новых переменных имеет вид :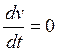. Значит, v не зависит от t и решение можно записать в виде: (10)

Т.е. .

F- произвольная функция заданного аргумента, Т.е. решение  (3) имеет вид (10), где F- произвольная функция, а K(x,y)- правая часть соотношения (8).

С другой стороны, если мы каким-то образом сможем определить функцию , которая обращается в постоянную вдоль интегральной кривой уравнения  (6), т.е. вдоль характеристики, то в новых переменных  и t, эта кривая (функция) будет функцией только переменной .

.

А поскольку в (10) F – произвольная функция, то решение (10):  (11)

То есть, согласно соотношению (10) или (11), общее решение уравнения в частных производных, т.е. уравнения (3) зависит от произвольной функции, то есть содержит более высокую степень произвола, чем обычное ДУ.

Рассмотрим, как из всего множества решений можно выбрать единственное.

Пусть дана некоторая кривая g₁, которая задана параметрически: . Эта кривая не совпадает с характеристикой ни на одном интервале положительной длины. Зададим на этой кривой дополнительное условие:

                     (12)

w(s) – заданная функция параметра s. Задача (3) с условием (12) называется начальной задачей или задачей Коши, т.к. g₁ не характеристика, функция K(x,y) вдоль этой кривой будет меняться:

, то есть при наличии некоторых условий можно определить s как функцию от x:

.

Значение функции u в точке x на кривой g₁ и есть . Если теперь через точку x кривой g₁ провести характеристику, то ее уравнение будет таким: . А значение решения в точках характеристики будет:     (13)

Так как через каждую точку области G проходит характеристика, то эта формула и будет выражением для решения в любой точке области G.

         (13)

Замечания:

1. Вместо характеристики K(x,y) можно использовать функцию j(x,y).
2. Для того, чтобы получить зависимость s=W(x), надо, чтобы x вдоль кривой g₁ зависело от параметра s монотонно.
3. В этом случае функция W определяется однозначно.

ПРИМЕР.

,

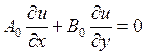A₀, B₀  - константы, тогда в соответствии с (5), (6), характеристика будет определяться дифференциальным уравнением:

,

,

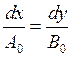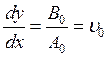 (в соответствии с определением характеристики).

Уравнение характеристики .

А значит, общее решение уравнения в частных производных имеет вид: u(x,y)=F(y-u₀x). F(y-u₀x) называется бегущей волной со скоростью u₀ и профилем F(y).

Для того, чтобы построить единственное решение, зададим дополнительное условие (12) :

u(x, q) = m(x), и кривую g₁:  и  (s - параметр).

Тогда: ,

, тогда

.

.

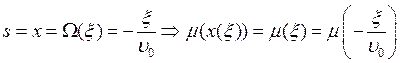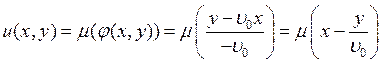То есть решение будет бегущей волной, профиль которой определяется заданной функцией m(x).

Для решения уравнения со многими переменными используется аналогичный подход. Если рассмотреть многомерный случай, тогда для определения характеристик получаем систему уравнений:

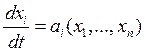, i=1,…,n.  (14)

Соответствующая форма траектории будет иметь вид:

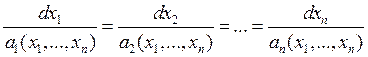     (15)