Методы теории возмущений. Бифуркации., страница 6

Тогда интегральные кривые системы уравнений (14)  называются характеристиками уравнения в частных производных (1). В силу того, что все a_i одновременно не равны нулю, для системы (14) выполняются условия теоремы и !, а значит, через каждую точку n-мерной области G проходит одна и только одна характеристика.

Теорема 1.

Вдоль характеристики решение уравнения (1) u(x₁,…,x_n) сохраняет постоянное значение.

Доказательство.

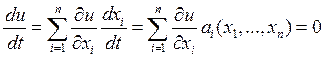 Þ u=const.

Идея построения общего решения уравнения – это обобщение двумерного случая. Строим семейство характеристик , соответствующее параметру t. Рассуждаем аналогично. Введем понятие первого интеграла:

Первым интегралом системы (15) называется функция j(x₁,…,x_n), которая обращается тождественно в постоянную, когда точка n-мерного пространства x пробегает интегральную кривую системы (15). Это означает, что новые функции  есть ни что иное, как первый интеграл, но, в свою очередь, первыми интегралами могут быть не только эти функции.

Пусть определены n-1 первых интегралов системы (15): j_i(x₁,…,x_n), i=1,…,n-1, и при этом матрица Якоби для этих функций не равна 0 в области G, то есть эти функции функционально независимы.

Обозначим это свойство за  в области G               (*)

Теорема 2.

Всякое решение y_i(x₁,…,x_n) уравнения (1) является первым интегралом системы (15) и, обратно, всякий первый интеграл системы (15) будет решением уравнения (1)

Доказательство.

Прямое утверждение доказывается теоремой 1, если заменить u на y. Обратное утверждение докажем.

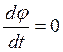Из теоремы 1, в  (16) заменим u на j, . Значит,  (**).

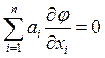j - первый интеграл (15) . Выполнение последнего равенства можно гарантировать вдоль характеристики. Для того, чтобы j было решением уравнения (1) необходимо показать, что это (**) выполняется для всей области G. Поскольку известно, что через каждую точку области G проходит характеристика, причем единственная, то это значит, то если (**) выполняется для характеристики, то оно будет выполняться на всех точках области G.

Теорема 3.

Всякое решение задачи (1): u = y(x₁,…,x_n) может быть представлено в виде:

u = y(j₁(x₁,…,x_n),…, j_n-1(x₁,…,x_n))= y(j₁,…,j_n-1)          (17)

y(j₁,…,j_n-1) – некоторая функция своих аргументов, которая дифференцируема по ним. j_i – первый интеграл системы (15), удовлетворяющий соотношению (*).

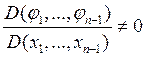 в G (немного другая запись)        (*)

(n-1) будет из-за того, что матрица квадратная.

Доказательство.

Функция y и функции j_i  в соответствии с теоремой 2 будут удовлетворять решениям уравнения (1), а, значит, они будут удовлетворять соотношению:

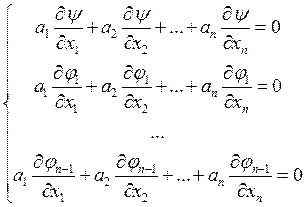          (18)

В каждой точке области G это соотношение (18) можно рассматривать как СЛАУ относительно коэффициентов a₁, a₂, …, a_n. По условию, 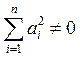, то есть у этой системы существует нетривиальное решение. Следовательно, определитель этой системы равен нулю всюду в области G или, другими словами,

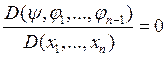 в G.

Значит, между функционалами j_i существует функциональная зависимость, а в силу соотношения (*) эта зависимость может быть представлена в виде соотношения (17). y(j₁,…,j_n-1). Ч.и.т.д.

Построенные дополнительные условия позволяют из множества всех решений выбрать единственное. Это условие формулируется также, как и в двумерном случае. Функция u задается на некоторой кривой g₁.

                 (19)

Тогда задача (1) с дополнительным условием (19) является задачей Коши для ДУ в частных производных. Решение ее в общем виде ищем как и для двумерного случая.

Квазилинейные уравнения

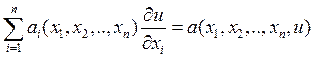              (2)

Рассмотрим квазилинейное уравнение (2). Решением этого уравнения будем называть функцию аргументов x₁,…,x_n, у которой существуют частные производные по всем аргументам и которая обращает соотношение (2) в тождество.

Введем новую функцию u, которая позволит сопоставить уравнению (2) следующее линейное уравнение:

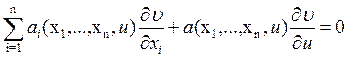             (1)

Теорема 1.

Введем функцию u=u(x₁,…,x_n,u). Пусть u - решение уравнения (1). А уравнение вида u(x₁,…,x_n,u)=0 – неявное задание функции.