![]()
Пусть в задаче заданы краевые условия:
![]()
![]()
Аппроксимируем на 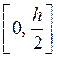 консервативной схемой:
консервативной схемой:
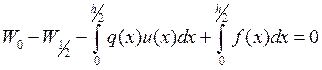
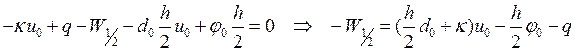
Поскольку центральная разность для полуцелой точки является
правой разностью для целой (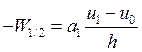 ), то:
), то:
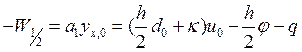
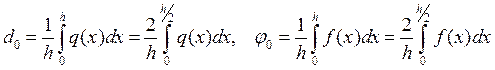
Т.о. разностная схема с краевыми условиями , имеет 2-ой порядок аппроксимации.
Рассмотрим функционал от ![]() :
:
![]()
Для ![]() ,
определенной на
,
определенной на ![]() принимает некоторое значение.
принимает некоторое значение.
Рассмотрим задачу: определить кривую
![]() , которая проходит через
, которая проходит через ![]() и
и ![]() и
минимизирует функционал . Пусть
и
минимизирует функционал . Пусть ![]() известная функция.
известная функция.
Пусть ![]() ,
, ![]() . Рассмотрим
. Рассмотрим ![]() -
удовлетворяет тем же краевым условиям, что и
-
удовлетворяет тем же краевым условиям, что и ![]() и
и ![]() . Тогда
. Тогда ![]() . Это
значит, что
. Это
значит, что ![]() можно рассматривать как скалярную функцию
от
можно рассматривать как скалярную функцию
от ![]() . Рассмотрим
. Рассмотрим ![]() :
: 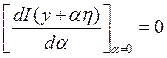 – условие минимума. Распишем в явном виде:
– условие минимума. Распишем в явном виде:
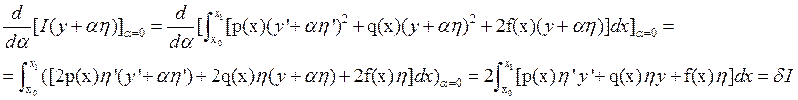
где![]() -вариация
функционала.
-вариация
функционала.
Если ![]() функционал
минимизирован.
функционал
минимизирован.
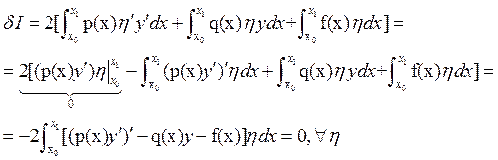
![]()
Определение: Уравнения, которым удовлетворяют экстремальные кривые (1.4), называются уравнениями Эйлера для данной вариационной задачи.
Если ![]() решения
уравнения доставляют абсолютный минимум уравнению .
решения
уравнения доставляют абсолютный минимум уравнению .
Пусть ![]() -
решение , а
-
решение , а ![]() - функция, удовлетворяющая тем же краевым
условиям, что и
- функция, удовлетворяющая тем же краевым
условиям, что и ![]() . Определим
. Определим ![]() ,
, ![]() .
Оценим приращение
.
Оценим приращение ![]() :
:
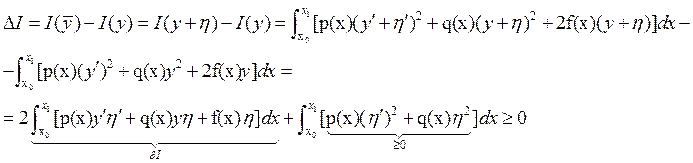
т.е. при заданных ограничениях
функция ![]() доставляет абсолютный минимум функционалу .
доставляет абсолютный минимум функционалу .
Рассмотрим задачу об определении
минимума функционала ![]() . Не налагая никаких ограничений
на
. Не налагая никаких ограничений
на ![]() - при так называемых естественных
условиях. Ход рассуждений остается тем же, но мы не можем воспользоваться
условием
- при так называемых естественных
условиях. Ход рассуждений остается тем же, но мы не можем воспользоваться
условием ![]() . Тогда при взятии интеграла по частям:
. Тогда при взятии интеграла по частям:![]() Тогда
Тогда ![]() .
.
![]() при
при ![]()
Чтобы учесть краевые условия, перепишем функционал в виде:
![]()
Если для аналогично вычислить ![]() , то мы получим, что минимум
, то мы получим, что минимум ![]() достигается при решении уравнения с краевыми условиями:
достигается при решении уравнения с краевыми условиями:
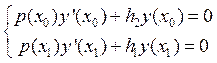
Линейное пространство ![]() называется НОРМИРОВАННЫМ, если на
множестве его элементов определена вещественная функция-норма
называется НОРМИРОВАННЫМ, если на
множестве его элементов определена вещественная функция-норма ![]() , которая удовлетворяет следующим аксиомам:
, которая удовлетворяет следующим аксиомам:
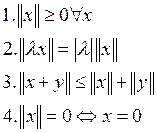
Замечания
![]()
Нормированное пространство X называется СТРОГО НОРМИРОВАННЫМ, если в 3-ей аксиоме
равенство возможно только для ![]()
Лемма
Для того чтобы
норма в пространстве ![]() была строго выпуклой, необходимо
и достаточно, чтобы пространство
была строго выпуклой, необходимо
и достаточно, чтобы пространство ![]() было строго
нормированным.
было строго
нормированным.
На одном и том же пространстве можно ввести несколько норм.
Полное нормированное пространство называется БАНАХОВЫМ.
Лемма
В банаховом пространстве из абсолютной сходимости ряда следует обычная сходимость, причем справедливо:
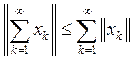
Система ![]() в
банаховом пространстве
в
банаховом пространстве ![]() , где
, где ![]() принадлежит
некоторому счетному множеству, называется полной в этом пространстве,
если замыкание ее линейной оболочки этой системы совпадает со всем
пространством.
принадлежит
некоторому счетному множеству, называется полной в этом пространстве,
если замыкание ее линейной оболочки этой системы совпадает со всем
пространством.
Последовательность элементов ![]() из банахова пространства B
называется базисом, если для любого элемента
из банахова пространства B
называется базисом, если для любого элемента ![]() существует
и при том единственная последовательность чисел
существует
и при том единственная последовательность чисел ![]() , такая
что
, такая
что 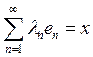 (1).
(1).
Лемма: Если система ![]() образует базис, то эта система будет
полной и линейно независимой.
образует базис, то эта система будет
полной и линейно независимой.
Пространство ![]() со скалярным произведением называется гильбертовым,
если оно полно в норме, порождаемой этим скалярным произведением.
со скалярным произведением называется гильбертовым,
если оно полно в норме, порождаемой этим скалярным произведением.
Лемма: Гильбертово пространство является строго нормированным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.