Траектории ЛА. Уточнённый метод Эйлера. Расчёт движения по направляющим. Расчёт траектории баллистических ракет и ракет-носителей космических ЛА, страница 9

21.10.2005г

На вертикальном участке траектории при 0tt1 интегрируется первое и третье уравнения системы (5). На этом участке 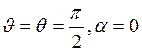, поэтому второе уравнение не рассматривается. На участке t1tt3  угол атаки задаётся в соответствии с зависимостью (4), интегрируются совместно первое, второе и третье уравнения. В результате находится .  определяется по формуле (4). После определения =(t)+ , находим программный угол тангажа совместным интегрированием первого, второго и третьего уравнений системы (5).

После момента t3  для tt3  , угол тангажа на участке [t3   tk] равен .  - задаётся. Зависимость  используется как статическое соотношение для определения угла атаки , где  также обычно задаётся заранее, исходя из необходимости получения максимальной или заданной дальности.

;

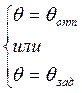>0, а значение  или  определяется из расчёта пассивного участка траектории БР с использованием результатов эллиптической теории.

После нахождения всех переменных и программных значений из четвёртого уравнения найдём - продольную координату. .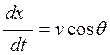

В литературе приводится следующая зависимость, хорошо аппроксимирующая результаты описанного выше алгоритма нахождения программы.

  ;

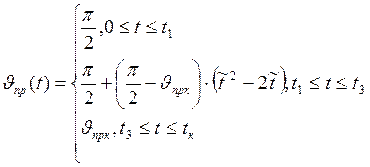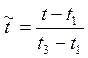 - относительное время полёта на криволинейном участке;

01  .

На рис.3 показан характер программной траектории одноступенчатой БР на активном участке.

На этом же рисунке показано взаимное расположение оси х1 и вектора скорости центра масс v.

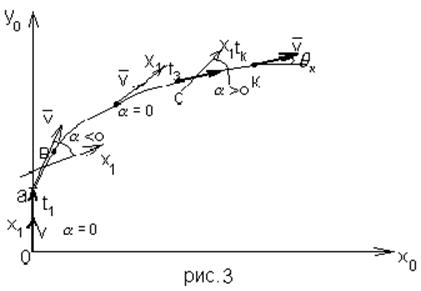
Как видно из рис.3, программная траектория одноступенчатой БР на активном участке состоит из следующих участков:

1)  вертикальный участок оа: =0, =;

2)  участок «завала» ав: <0, ;

3)  участок разворота вс: =0, ;

4)  участок «наведения» ск: >0, ;

Первые три участка лежат в плотных слоях атмосферы, где скоростной напор мал. На этом участке происходит осечка работы двигателя, и траектория выдерживается близкой к прямолинейной, ориентированной к горизонту под некоторым заданным или оптимальным углом бросания .

Формируем постановку задачи выбора программы наибольшей дальности.

Задача сводится к трёхпараметрической экстремальной задаче. Варьируется три параметра:  . Обозначим вектор этих параметров буквой С().

Требуется определить компоненты вектора , при которых реализуется максимум критерия оптимальности J=L(C), где L - полная дальность полёта БР.

                                                   (6)

при этом должны выполняться ограничения на нормальные перегрузки, углы атаки, вес и т.д.

В число ограничений может включаться и величина ошибки в дальности полёта в конце траектории.

Ограничение в векторной форме можно записать в виде:

G 0                                                                                          (7)   

G = 

j - число принимаемых ограничений;

 - заданные численные значения ограничений;

Область выбора параметров вектора  задаётся в виде векторного неравенства   асв                                                                                              (8), где а и в - m - мерные векторы предельных значений параметров вектора .

Таким образом, в такой постановке допускается, что дальность L и все ограничения могут быть определены при конкретных значениях вектора.

Указанные функции определяются интегрированием системы уравнений БР на активном участке и использованием формулы, определяющей полную дальность полёта: L=xa+Ln, где хa - дальность активного участка;

Ln - дальность пассивного участка; 

Для определения дальности Ln существуют приближённые формулы, которые основываются на выводах эллиптической теории.

Для решения поставленной задачи можно использовать численные методы нелинейного математического программирования. В основе этих методов лежит итерационный процесс, который заключается в следующем: вначале, в качестве нулевого приближения , на основании предварительных исследований или статистики, задаются конкретными значениями вектора параметров С=С(0). Далее этот вектор последовательно улучшается с использованием рекуррентного соотношения: