Траектории ЛА. Уточнённый метод Эйлера. Расчёт движения по направляющим. Расчёт траектории баллистических ракет и ракет-носителей космических ЛА, страница 8

В конце траектории активного участка при  угол  должен быть равен некоторому конечному значению , который определяется исходя из необходимости обеспечения заданной или максимальной дальности полёта. При этом на завершающем отрезке активного участка угол тангажа  выдерживается постоянным или близким к постоянному, а также обеспечивается прямолинейный участок траектории под углом возвышения , величина которого вместе с конечной скоростью  определяет требуемую или максимальную дальность полёта. Выключение двигателя на прямолинейном участке траектории уменьшает влияние возмущений, связанных с остановкой двигателя на отклонение двигателя на расчётной траектории. Далее выдвигаются требования, чтобы нормальная перегрузка находилась в заданных пределах на всём активном участке.

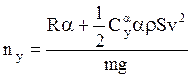
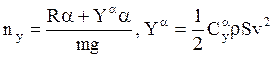
Эти нормальные перегрузки регламентируются условиями жёсткости конструкции и прочности ракеты. Определяющее влияние  имеет угол атаки . Поэтому для уменьшения  необходимо стремиться к программе с возможно меньшими углами атаки , особенно на тех участках траектории, где скоростной напор 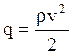 имеет существенное значение.

Участки траектории с большими скоростными напорами q необходимо проходить с нулевыми или минимальными углами атаки . На участках траектории, где скоростной напор мал (ближе к концу активного участка) угол  может быть увеличен. Вид зависимости  и  должен учитывать также эффективность работы органов управления. В области трансзвуковых скоростей  происходит резкое увеличение коэффициентов  и , что отрицательно сказывается на работе СУ.

()

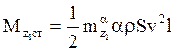Контур управления рассчитан на определённое значение этих параметров и их резкое изменение может привести к ухудшению качества процесса управления угловым движением. Чтобы избежать этого отрицательного влияния, можно изменять параметры контура управления, т.е. адаптировать контур управления к изменяющимся условиям полёта (адаптивный автопилот). Использование адаптивного автопилота усложняет структуру СУ. Для уменьшения влияния этих резких изменений  и  необходимо, чтобы БР проходила указанную область чисел М с нулевыми или близкими к нулю . Отмеченным условиям хорошо удовлетворяет следующая программа изменения угла атаки  при движении в плотных слоях атмосферы.

               (4)

где  - предельное значение угла  на дозвуковом участке траектории, а  - время от точки старта до конца вертикального участка полёта (продолжительность вертикального участка), а – постоянный коэффициент, обычно подбираемый для данного класса ракет так, чтобы при достижении  получить угол . Время, при котором достигаются эти значения маха, обозначим . Параметры  и  могут варьироваться при выборе оптимальной программы. Траектория наиболее чувствительна к величине . Зависимость (4) задаёт  в виде кривой, которая быстро достигает своего максимума (по абсолютной величине), а затем убывает: сначала быстро, а по мере увеличения времени t – медленнее, стремясь к нулю при . Типичные графики  и  для активного участка траектории одноступенчатой БР при вертикальном старте представлены на рисунке 2.

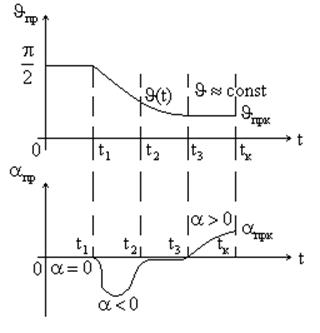
Рисунок 2

Таким образом, траектория БР на активном участке может быть разбита на 3 участка:

1)

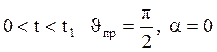
2)    - плавная зависимость, изменяется от  до , соответствующего данной дальности полёта L, причём на этом участке угол  изменяется в соответствии с зависимостью (4). Время  характеризует момент достижения чисел .

3)   - это участок движения БР в относительно разряжённых слоях атмосферы при небольших значениях скоростного напора 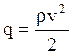, когда можно принять . Необходимый для обеспечения программы движения .

Порядок выбора зависимости  и порядок расчёта программной траектории.

При расчётах программной траектории и выбора программы угла тангажа используется система уравнений (5):

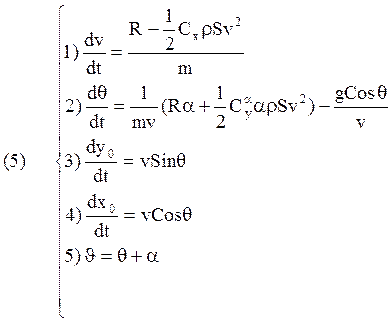
При этом  считаются известными, . Четвёртое уравнение, определяющее закон изменения продольной координаты  при выборе программной зависимости не используется, т.к. координата  не входит в остальные уравнения системы (5). Задача решается численным интегрированием по участкам траектории.