Траектории ЛА. Уточнённый метод Эйлера. Расчёт движения по направляющим. Расчёт траектории баллистических ракет и ракет-носителей космических ЛА, страница 3

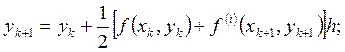
i - номер итерации;

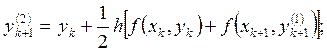
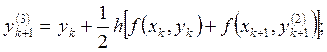
;  к=0,1,2,…

R;

;

Метод Рунге - Кутта.

В методе Рунге-Кутта истинная интегральная кривая заменяется параболой того или иного вида. Метод Рунге-Кутта основан на формуле парабол Симпсона. Формула Симпсона определяет интеграл:

 

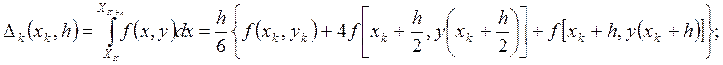
Алгоритм метода Рунге-Кутта(для одного дифференциального уравнения, записанного в нормальной форме Коши):

+к;

            к=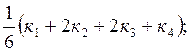

 

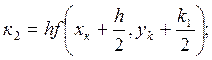
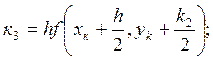
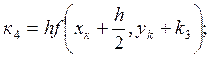
R

Рассмотрим алгоритм метода Рунге-Кутта для системы дифференциальных уравнений п - го порядка.

Имеется система дифференциальных уравнений, записанных в нормальной форме Коши:

h - шаг интегрирования;

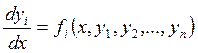                                                                                               (1)

                                                                                                             (2)

х	y1	y2	...	Yn
х0				yn0
х1
х2
х3
.
.
.
				xk+1=xk+h

+к;

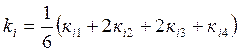, где

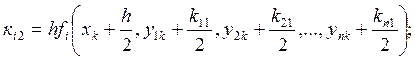
1-ый индекс - номер функции;

2-ой индекс - номер ;

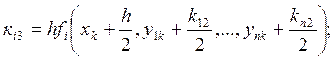
  Задача:   Рассмотрим случай, когда система состоит из двух уравнений:

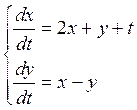                          при   t=0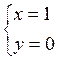  

h=t=0.2

                

                     

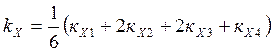
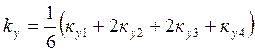
  =h[]

  =h[]

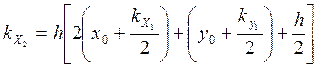, так как

  

 

 

 

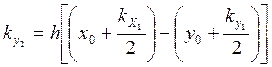
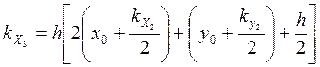
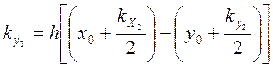
Расчёт траектории неуправляемых реактивных снарядов ближнего действия.

При расчёте траектории неуправляемых реактивных снарядов, принимается за материальную точку переменной массы, которая совпадает с центром масс. Это эквивалентно допущению, что вращательное движение относительно центра масс не влияет на движение центра масс. Такая траектория является идеальной.

Расчёт активного участка траектории:

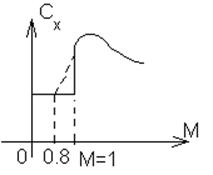
Рассматривается движение вертикальной плоскости - плоскости стрельбы. Поле силы тяжести принимается постоянным  параллельным. Тяга R принимается постоянной и не зависящей от высоты полёта. Угол атаки , . Раз, значит подъёмная сила  

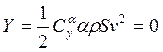
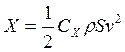 , причём , так как.

Сила тяги определяется по формуле R=uQ, где u=Pуд*g - скорость истечения продуктов сгорания.

Pуд=280-320 [сек]

G=mg;

Векторное уравнение движения точки:

 

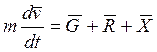
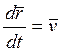, где  - радиус- вектор центра масс относительно начальной точки;

, где i =const- коэффициент формы;

 - закон сопротивления;

В баллистике рассматривают следующие законы сопротивления:

1) закон Сиаччи;

2) закон 1930г (Гарнье);

3) закон 1943г (снаряд морской артиллерии «Куард»);

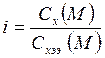
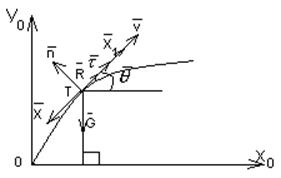
Рассмотрим уравнение для расчёта траектории. Воспользуемся векторным соотношением.

 - орт касательной;

 - орт нормали; х1 - ось ЛА.

16.09.05 *

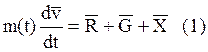
1)

2) - оси сопровождающего трёхгранника

 - угол наклона траектории (угол возвышения)

Точка 0 – точка схода ЛА с направляющих

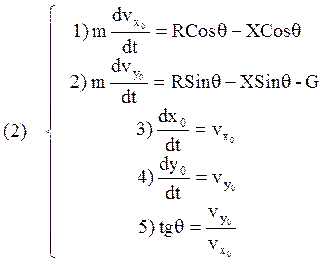
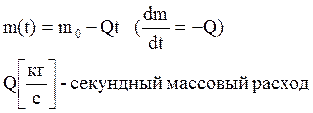
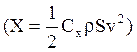
Начальные условия:

(3) При t=0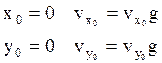  

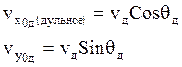
 - скорость схода с направляющих

 - угол наклона направляющих пусковой установки

Можно использовать :

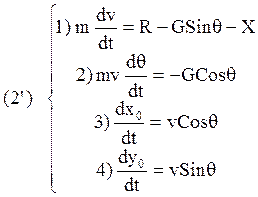
(3’) При t=0  

 - переменные системы (2’)

Основной метод решения  системы (2) или (2’) – численное интегрирование. Наряду с методом численного интегрирования в данном случае при расчёте активного участка может быть использован приближённый аналитический метод. Этот метод основан на методе последовательных приближений (метод Пикара), известном в теории дифференциальных уравнений. Основная идея метода Пикара заключается в следующем.

Имеется дифференциальное уравнение, записанное в векторной форме

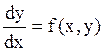, где y – вектор, f – заданная вектор-функция

При

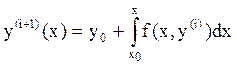
 - номер итерации

Условия Липшица.