Траектории ЛА. Уточнённый метод Эйлера. Расчёт движения по направляющим. Расчёт траектории баллистических ракет и ракет-носителей космических ЛА, страница 10

С(+1)=С()+С()                                                                   (9), где

=0, 1, 2.. - номер итерации;

С () - вектор поправок, определяемый из условий, чтобы критерий оптимальности монотонно приближался к экстремальному значению L (+1)  L(), а также выполнялись на каждой итерации заданные ограничения (7) и (8).

Этот метод поправок С ()  можно найти методом случайного поиска или одним из градиентных методов наискорейшего спуска.

Приближённая постановка задачи расчёта программной траектории.

Сущность этой постановки основывается на учёте малости при полёте по программной траектории, поэтому вместо программной зависимости  используют зависимость (t). В этом случае программа может быть представлена зависимостью:

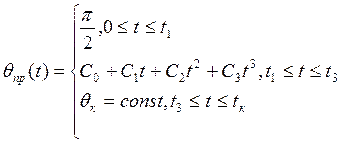                                            (10)

Коэффициенты  определяются из требований , предъявляемых к программной траектории в различные моменты времени.

Предъявим следующие требования:

                                                                              

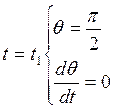
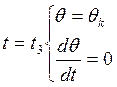
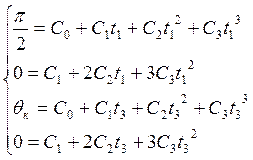                                                              (11)

Отсюда находим .

Для расчёта программной траектории используется следующая система уравнений:

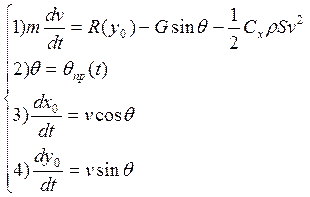                                                    (12)

Известны: .

Задача решается численным интегрированием. Помимо этого метода при решении задачи может быть использован приближённый аналитический метод, основанный на методе итераций, как при решении траектории на активном участке (метод Королёва).

28.10.05 *

Особенности программы для двухступенчатых и многоступенчатых ракет.

Для двухступенчатой БР примерная программа изменения угла тангажа для второй ступени имеет следующий вид:

, где

- начальное значение угла тангажа второй ступени;

- время, соответствующее ;

 - угловая скорость угла тангажа, задаётся исходя из конструктивных особенностей ракеты.

Очень часто  и  не совпадают. В этом случае должен быть обеспечен плавный и возможно быстрый переход от  до , где - время окончания работы первой ступени, соответствующее , при постепенном переходе к прямолинейному участку траектории, на котором заканчивается работа второй ступени. Оптимальный угол  на прямолинейном участке траектории в конце работы второй ступени обеспечивает максимальную дальность.

График изменения угла тангажа для двухступенчатой БР можно представить следующим образом:

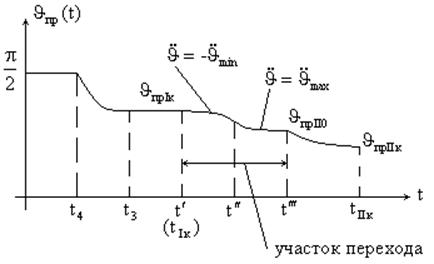
На всех ступенях, начиная со второй , где  - угол тангажа, соответствующий началу работы i-ой ступени (i=2,3…). Отступление от этой зависимости приводит лишь к потере дальности.

 

Расчёт пассивного участка траектории БР и ракет-носителей космических аппаратов

Рассмотрим характер баллистической траектории БР от старта до точки падения. Траектория БР соизмерима с размерами Земли:

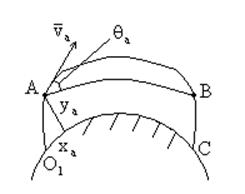
 - активный участок

ABC – пассивный участок

АВ – основная часть пассивного участка, расположенная в разряжённых слоях атмосферы

ВС – ветвь ВС расположена в плотных слоях атмосферы (на уровне высоты активного участка).

Исходными данными являются данные конца активного участка .

Для расчёта основной части пассивного участка, расположенного в разряжённых слоях атмосферы, используются выводы так называемой эллиптической теории. Участок ВС рассчитывается с учётом сопротивления воздуха и кривизны Земли.

Основные допущения эллиптической теории

1. Пренебрегаем сопротивлением атмосферы, а также всеми космическими силами (например, световым давлением). ЛА рассматривается как материальная точка с постоянной массой.

2. Движение точки рассматривается в центральном поле земного тяготения, т.е. в каждой точке траектории сила тяготения направлена к центру Земли, кривизна которой учитывается и зависит от расстояния до этого центра. Величина силы земного тяготения определяется законом всемирного тяготения.