Траектории ЛА. Уточнённый метод Эйлера. Расчёт движения по направляющим. Расчёт траектории баллистических ракет и ракет-носителей космических ЛА, страница 14

1)

2)  расположен в абсолютной плоскости стрельбы

- компланарны (лежат в одной плоскости)

3) угол между векторами  равен

Из 1):

Из 2):

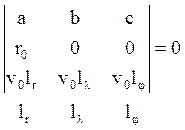
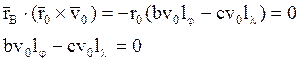
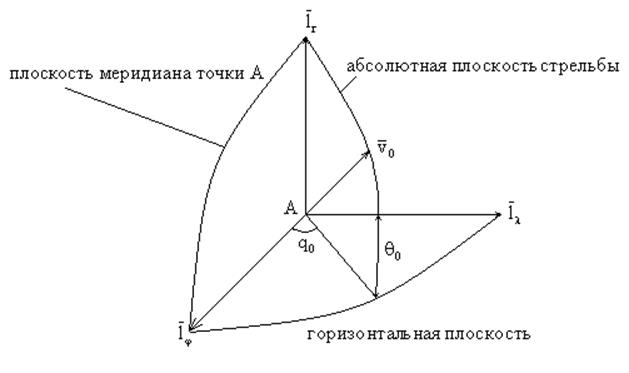
- угол, ориентирующий абсолютную плоскость стрельбы по отношению к плоскости меридиана точки А

;   

Из 3): ;  

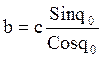
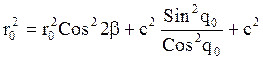
Для определения широты спроектируем  на ON:

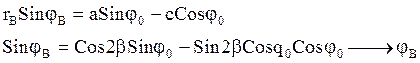
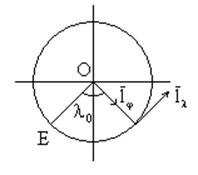
Для определения  спроектируем  на OE:

,   

В этой задаче параметры точки А   известны.

25.11.05г

Определение вектора абсолютной скорости БР в конце активного участка.

В результате расчё1та активного участка траектории БР были получены параметры движения относительно неподвижной земли  - параметр, определяющий ориентацию плоскости стрельбы относительно плоскости меридиана, проходящей через точку А. Во все формулы эллиптической теории входят параметры движения относительно инерциальной системы координат . Возникает задача, как определить параметры абсолютного движения с индексом ноль, зная параметры относительно земли. Для решения этой задачи обратимся к сферической системе координат с ортами  с началом в точке А. На следующем рисунке показана плоскость начального меридиана, проходящей через точку А.

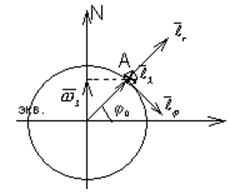
Благодаря суточному вращению Земли со . Абсолютная скорость точки А отличается от абсолютной скорости относительно Земли.

                                                                                                                                        (1)

 - направлена по орту ;

;

 - скорость точки относительно Земли;

 - скорость точки А относительно инерциальной системы координат;

 - скорость точки А за счёт вращения Земли, это скорость в переносном движении;

;

Если считать, что , =0, (то есть точка А на экваторе), то . В этом случае .

Определим величину и ориентацию скорости . Для этого обратимся к системе координат:

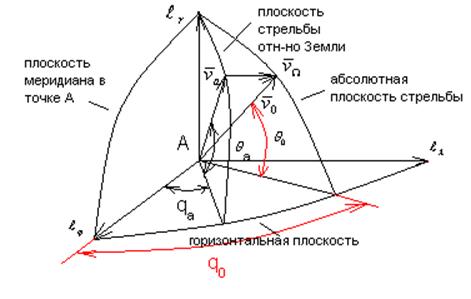
Запишем векторное равенство (1) в проекциях на , мы получим:

                                                        (2)

На основании этого выражения мы найдём все требуемые величины, а именно:

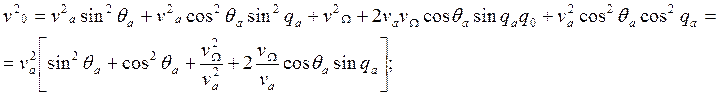
Для того, чтобы найти  и  обратимся к векторному равенству (1). Спроектируем векторное уравнение (1) на направление

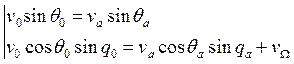                                                                                                               (3)

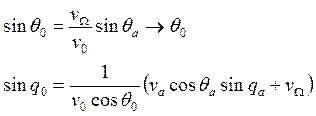
(4)  

Пусть (широта точки А) равна нулю, тогда , =7000 м/с, .

=7400м/с;

=28;

= 4,1;

При таких расчётах нужно учитывать различие между параметрами абсолютного и относительного движения при определении начальных условий точки А.

Система уравнений неуправляемого движения ЛА при спуске в атмосфере планеты с учётом кривизны её поверхности. 

Эта система уравнений может быть использована при расчёте участка БС нисходящей ветви пассивного участка БР, расположенной в плотных слоях атмосферы.

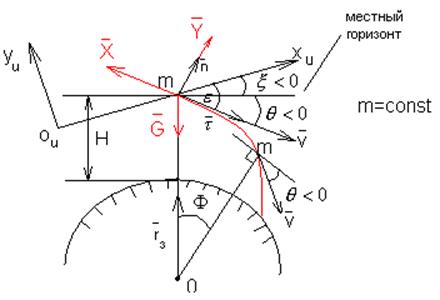
Ориентируем местный горизонт в инерциальной системе координат.

 - орт касательной;

n - орт нормали к траектории;

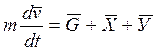                                                                                                                             (1)

G=mg

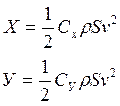
Запишем векторное уравнение (1) в проекциях: 

=

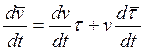
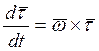
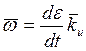
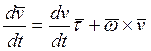
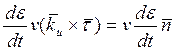
Значит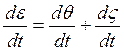

 - угол, ориентирующий скорость изменения поворота;

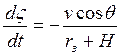
Таким  образом, мы получаем, что ;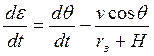

;

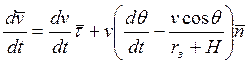Запишем векторное уравнение (1) в проекциях на касательную и нормаль:

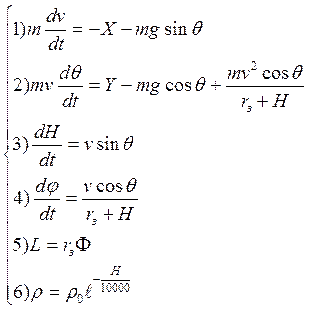                                                                                  (2)

 - массовая плотность на поверхности Земли;

Система (2) решается численным интегрированием, определяются:

Начальные условия:  t=0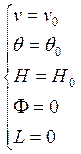 

Кроме численного интегрирования, для решения системы (2) имеются приближённые аналитические методы, см. например, литературу Д.Р. Чеплин  Приближённый аналитический метод исследования входа тел в атмосферы планет.  М.1962.

Особенности траектории спуска.

При спуске с высоты, порядка 100-120км, массовая плотность воздуха в начальный момент сравнительно мала. Затем при приближении к Земле, она (массовая плотность) резко возрастает.

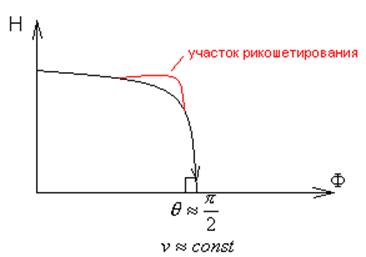
Имеется участок квазистационарного спуска. Если ЛА обладает качеством (к=), то могут быть участки рикошетирования.