3. Движение рассматривается в инерциальной с.к., неподвижной
относительно звёзд. Начало этой системы помещается в центре Земли. Орбитальное
движение Земли не учитывается, но учитывается суточное вращение Земли.
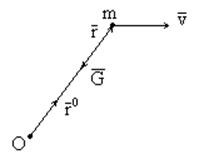
Плоскость стрельбы в этой с.к. будем называть абсолютной плоскостью стрельбы.
Абсолютная плоскость стрельбы – это плоскость, проходящая через вектор начальной
абсолютной скорости и радиус-вектор точки конца активного участка относительно
центра Земли. Заметим, что вектор начальной абсолютной скорости ![]() не равен скорости в конце активного
участка
не равен скорости в конце активного
участка ![]() , которая получена из расчёта активного
участка без учёта вращения Земли. Связь между этими скоростями будет рассчитана
в дальнейшем.
, которая получена из расчёта активного
участка без учёта вращения Земли. Связь между этими скоростями будет рассчитана
в дальнейшем.
Векторное уравнение движения точки в условиях допущений эллиптической теории
На основании сформулированных допущений можно сформулировать:
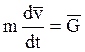 , где
, где
![]() - вектор абсолютной скорости
точки, т.е. скорость относительно инерциальной абсолютно неподвижной с.к.
- вектор абсолютной скорости
точки, т.е. скорость относительно инерциальной абсолютно неподвижной с.к.
![]()
![]() - абсолютное ускорение точки
- абсолютное ускорение точки
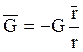 , где
, где 
![]()
Величина силы определяется законом всемирного тяготения:
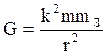
![]() - универсальная гравитационная
постоянная
- универсальная гравитационная
постоянная
m – масса точки
![]() - масса Земли
- масса Земли
r – расстояние от точки до центра Земли
![]() - гравитационный параметр Земли
- гравитационный параметр Земли
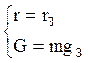
![]() - радиус Земли,
- радиус Земли, ![]() =6371 км
=6371 км
![]()

![]()

Учитывая выражение для ![]() подставляем
в векторное уравнение силу G:
подставляем
в векторное уравнение силу G:
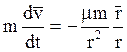 ,
, 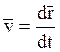
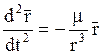 (1)
(1)
Из уравнения (1) видно, что траектория ЛА на пассивном участке в условиях допущения эллиптической теории не зависит от массы ЛА (следствие неучёта аэродинамического сопротивления), поэтому при одинаковых начальных условиях при любой массе ЛА траектории будут одинаковыми.
Перепишем уравнение (1) в проекциях. Обозначим Oxyz – инерциальная с.к., тогда:
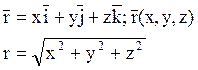
 (2)
(2)
Чтобы найти траекторию, надо найти зависимость координат как функцию времени x(t), y(t), z(t).
Система (2) является нелинейной и прямым интегрированием точное аналитическое решение найти не удаётся. В то же время, задача нахождения траектории при допущениях эллиптической теории имеет точное решение. Это решение можно найти косвенным путём, определив первые интегралы векторного уравнения (1).
Первые интегралы векторного уравнения движения
Понятие первого интеграла.
Если уравнение имеет вид ![]() , то
первым интегралом такого уравнения
, то
первым интегралом такого уравнения
n-ого порядка называется
соотношение, нетождественно равное постоянной между функцией и её производными
до n-1 порядка включительно ![]()
В теории дифференциальных уравнений доказывается, что знание первого интеграла позволяет понизить порядок на единицу без потери решения. А знание n независимых интегралов позволяет найти общее решение этого уравнения.
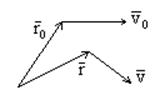
Приведём без вывода первые интегралы векторного уравнения (1) и сделаем выводы, исходя из этих интегралов:
1) Интеграл моментов количества движения (интеграл площадей)
![]()
![]() - момент количества движения относительно
центра Земли точки с единичной массой
- момент количества движения относительно
центра Земли точки с единичной массой
Он является математическим выражением второго закона Кеплера – закона постоянства секториальной скорости точки. Секториальной скоростью называется скорость изменения площади, ометаемой радиус-вектором точки при движении её по траектории.
Из этого уравнения следует вывод, что траектория является плоской кривой, расположенной в абсолютной плоскости стрельбы.
Если обозначить проекции вектора ![]() ,
, ![]() ,
, ![]() , то
можно записать уравнение в проекциях на оси x,y,z:
, то
можно записать уравнение в проекциях на оси x,y,z:
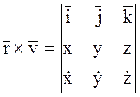
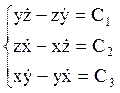 (3)
(3)
Т.к. ![]() , то
, то ![]() , записывая в проекциях, получим:
, записывая в проекциях, получим:
![]() (4)
(4)
Уравнение (4) является уравнением плоскости, в
которой происходит движение точки. Запишем выражение для модуля вектора ![]() :
:
![]()
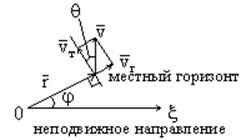
![]() - угол возвышения
- угол возвышения
![]()
![]() , где индекс 0 относится к точке
А (начальной точке).
, где индекс 0 относится к точке
А (начальной точке).
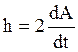 ,
, ![]() -
секториальная скорость
-
секториальная скорость
![]() - радиальная проекция скорости
- радиальная проекция скорости
![]() - трансверсальная проекция
скорости
- трансверсальная проекция
скорости
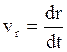 ,
, 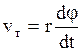
![]() ,
, ![]()
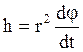 (5)
(5)
11.11.05г
Интеграл энергии.
Интеграл энергии - это скалярный интеграл:
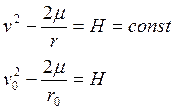 (6)
(6)
Закон сохранения механической энергии, при движении точки по орбите.
Интеграл Лапласа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.