При а=1 ![]() . Проинтегрируем:
. Проинтегрируем:
![]() или получаем
или получаем ![]() . Отсюда видно, что если
. Отсюда видно, что если ![]() , то это метод погони
(чистое преследование);
, то это метод погони
(чистое преследование);
если ![]() , то это метод погони с
постоянным углом упреждения.
, то это метод погони с
постоянным углом упреждения.
5) Уравнение метода параллельного наведения
![]() (6)
(6)
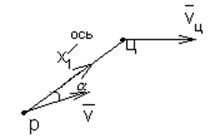
Запишем уравнения для расчёта кинематической траектории метода наведения двухточечного типа. Для этого, прежде всего, выведем основное кинематическое соотношение методов наведения двухточечного типа.
Пусть точка О - неподвижная.
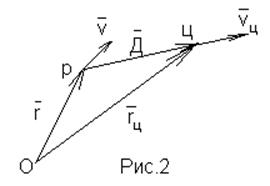
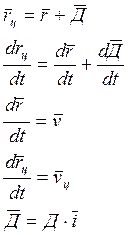
![]() - орт оси х, который совпадает с
вектором
- орт оси х, который совпадает с
вектором ![]() ;
;
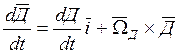
![]() - абсолютная угловая скорость
вектора
- абсолютная угловая скорость
вектора ![]() ;
;
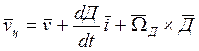 (7)
(7)
Спроектировав (7) на произвольные оси, можно получить уравнения для расчёта кинематической траектории ракеты на цель, движение которой известно.
Используем систему координат ху, см. рис.1. Определим
векторное соотношение![]() :
:
![]() , где
, где ![]() -
орт оси z, перпендикулярной плоскости (ху);
-
орт оси z, перпендикулярной плоскости (ху);
![]()
![]()
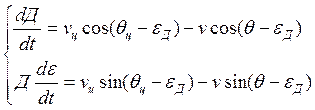 (8)
(8)
![]() - известны.
- известны.
Эта система уравнений содержит три неизвестных - ![]() . Чтобы замкнуть эту систему нужно добавить
уравнение метода:
. Чтобы замкнуть эту систему нужно добавить
уравнение метода: ![]() .
.
При произвольном движении (плоском) цели, эта система решается численным интегрированием, однако, в некоторых частных случаях удаётся получить аналитическое решение.
Если скорость ракеты неизвестна, то систему уравнений
(8) надо дополнить уравнениями, определяющими эту скорость. Приведём систему
уравнений для определения траектории ракеты, которая наводится на цель по
методу пропорционального сближения. Будем считать, что ![]() и
и
![]() - известные функции времени.
- известные функции времени.
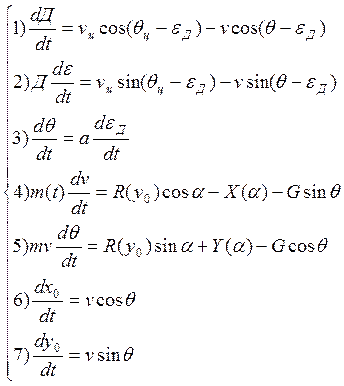 (9)
(9)
m=m(t)
![]()
Система (9) определяет следующие переменные: ![]()
![]() При этом
При этом
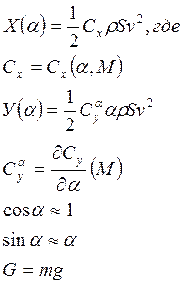
Примечание: Если удаётся угол атаки априори считать известным, равному среднему
значению, тогда из этой системы можно исключить пятое уравнение.
В случае пространственного движения система (8) и (9) усложняется. Система (8) будет состоять из трёх уравнений, а система (9) - из 11 уравнений.
Формула промаха ракеты для методов наведения двухточечного типа.
Понятие метода самонаведения тесно связана с точностью
наведения ракеты на цель, поэтому рассмотрим аналитическое выражение для
промаха ракеты. Промах - минимальное расстояние ракеты от цели, которое
достигается в процессе наведения. Система наведения проектируется так, чтобы
промах был наименьшим. Вводится понятие мгновенного промаха и фактического
промаха. Будем рассматривать плоское движение ракеты и цели в вертикальной
плоскости О![]() .
.
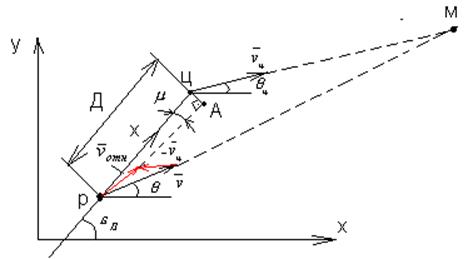
Пусть ракета в процессе движения к точке встречи с
целью (точки М), находится в некоторой точке Р в момент времени t. Параметры движения ракеты Р(![]() ) и цели
Ц(
) и цели
Ц(![]() ) в общем случае могут быть произвольными.
Введём понятие «мгновенный промах».
) в общем случае могут быть произвольными.
Введём понятие «мгновенный промах».
Мгновенный промах - это такое значение промаха, которое имело бы место в том случае, если бы начиная с данного момента времени t, полёт ракеты и цели на оставшемся до встречи участке траектории (точки М) происходил равномерно и прямолинейно.
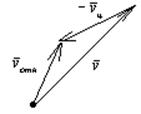
Для определения мгновенного промаха удобно рассматривать картину относительного движения. Введём вектор относительной скорости.
![]() (10)
(10)
 ЦА=h=Дsin
ЦА=h=Дsin![]()
При принятых допущениях о том, что, начиная с данного
момента времени t, величины ![]()
![]() , а
, а ![]()
![]() - постоянные, траектория ракеты
относительно цели будет пря мой линией РА. Промах определяется отрезком ЦА. Для
определения мгновенного промаха надо найти угол sin
- постоянные, траектория ракеты
относительно цели будет пря мой линией РА. Промах определяется отрезком ЦА. Для
определения мгновенного промаха надо найти угол sin![]() . Для этого спроектируем векторное
уравнение (10) на направление линии РЦ и на направление, перпендикулярное РЦ.
. Для этого спроектируем векторное
уравнение (10) на направление линии РЦ и на направление, перпендикулярное РЦ.
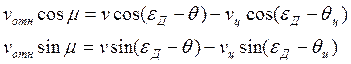 (*)
(*)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.