![]() - определяет форму траектории;
- определяет форму траектории;
р - определяет размер траектории;
![]() =0 - окружность;
=0 - окружность;
![]() =1 - парабола;
=1 - парабола;
![]() <1 - эллипс;
<1 - эллипс;
![]() >1 - гипербола;
>1 - гипербола;
Запишем выражение для эксцентриситета и фокального параметра р:
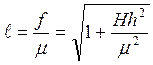 (14)
(14)
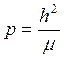 ;
;
![]() , р являются
постоянными параметрами для данной траектории и зависят от начальных условий.
, р являются
постоянными параметрами для данной траектории и зависят от начальных условий.
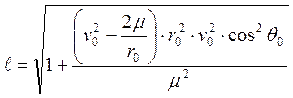 (14’)
(14’)
p= 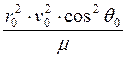
Характер траектории зависит от начальных условий ![]() . В зависимости от сочетания этих величин,
мы получим значение
. В зависимости от сочетания этих величин,
мы получим значение ![]() и р.
и р.
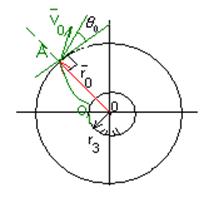
Различные виды траектории пассивного участка. Круговая (1-ая космическая) и параболическая (2-ая космическая) скорости.
В зависимости от значения ![]() реализуется
та или иная траектория.
реализуется
та или иная траектория.
1) Траектория окружность ![]() =0
=0
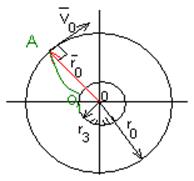
О1А - активный участок;
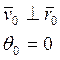
Определим необходимую скорость: ![]()
![]() (круговая
(круговая ![]() или
первая космическая
или
первая космическая ![]() ).
).
Полагая ![]() =0 в соответствии с
(14’) получаем
=0 в соответствии с
(14’) получаем
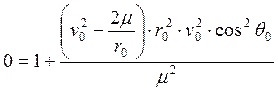
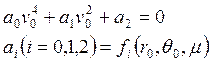
![]()
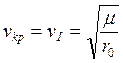 (15) - круговая или первая космическая скорость;
(15) - круговая или первая космическая скорость;
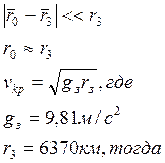
![]()
![]() 7,9км/с.
7,9км/с.
Если ![]()
![]() ,
то из формулы (14') получаем
,
то из формулы (14') получаем ![]() <1, то есть
траектория будет эллипсом.
<1, то есть
траектория будет эллипсом.
3) Траектория
параболы ![]() =1.
=1.
Выходит из поля земного тяготения. ![]() -
параболическая или вторая космическая скорость. Найдём её.
-
параболическая или вторая космическая скорость. Найдём её.
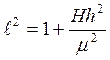
![]() =1, если
=1, если 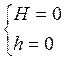
![]() =0;
=0;
h=![]() ;
;
h=0, ![]() =
=![]() , h
, h![]() 0, так как в противном случае
получаем прямую линию, а не параболу, значит
0, так как в противном случае
получаем прямую линию, а не параболу, значит ![]() .
.
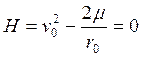
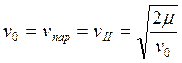 (16)
(16)
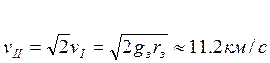
Если ![]() <1
- это траектория эллипс.
<1
- это траектория эллипс.
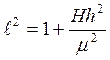
H<0, то есть 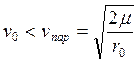 (17)
(17)
Это условие (17) является необходимым и достаточным,
чтобы траектория была эллипсом всегда. Если при этом 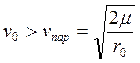 (18),
то этот эллипс является спутником Земли. Условие (18) является только
достаточным условием, так как спутник Земли может существовать и при
(18),
то этот эллипс является спутником Земли. Условие (18) является только
достаточным условием, так как спутник Земли может существовать и при ![]() . Это будет в том случае, если начальная
точка эллиптической траектории орбиты будет совпадать с апогеем.
. Это будет в том случае, если начальная
точка эллиптической траектории орбиты будет совпадать с апогеем.
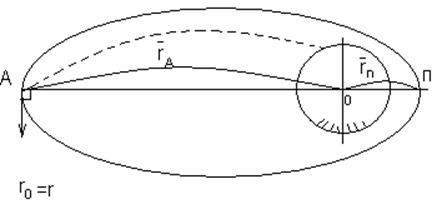
Точка А - апоцентр орбиты;
Ап - ось апсид.
18.11.05 *
е>1: траектория гипербола
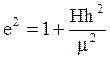
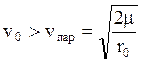
Н>0 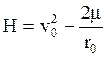
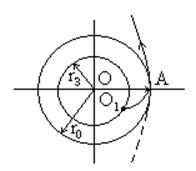
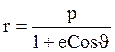
Расчёт эллиптической дальности БР. Оценка полной дальности пассивного участка. Оптимальный угол возвышения в конце активного участка. Время полёта.
Рассмотрим случай БР:
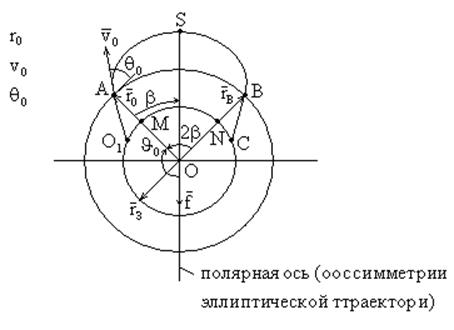
![]() - активный участок
- активный участок
ВС – часть пассивного участка
АВ – эллиптическая часть траектории
![]()
![]() - дальность активного участка
- дальность активного участка
![]()
![]()
![]()
Нам известны параметры точки А: ![]()
![]()
![]()
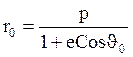 ;
; 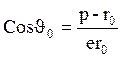
![]()
![]()
![]()
![]() - такой угол, при котором
эллиптическая дальность, а, следовательно, и полная дальность пассивного
участка максимальна.
- такой угол, при котором
эллиптическая дальность, а, следовательно, и полная дальность пассивного
участка максимальна.
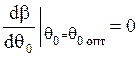
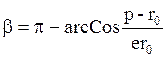
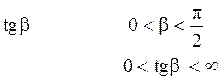
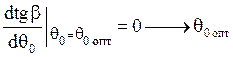
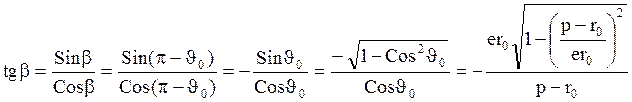
Подставляя в последнюю формулу значения p,e как функции начальных условий, после элементарных преобразований получаем:
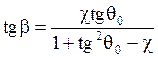 (17)
(17)
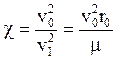
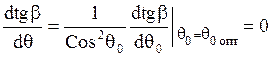 (18)
(18)
Вычисляя эту производную и приравнивая нулю, найдём:
![]() (19)
(19)
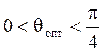 , т.к.
, т.к. ![]()
Если ![]() увеличивается, то
увеличивается, то ![]() ; если
; если ![]() уменьшается,
то
уменьшается,
то 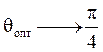 .
.
Найдём наибольшую дальность:
![]() при
при ![]()
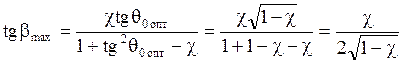 (20)
(20)
Определим время полёта:
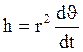 (из формулы (5) при
условии:
(из формулы (5) при
условии: ![]() )
)
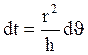
Т.к. эллиптическая траектория симметрична относительно полярной оси, то:
![]()
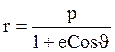
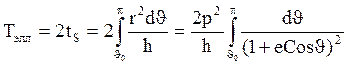
Интеграл берётся заменой 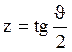
Точную формулу и выкладки можно найти в книжке: «Автоматизация расчёта траекторий» Шалыгин, Кабанов, Санников, Толпегин.
Если e<<1, то интеграл можно взять приближённо, разложив в ряд Тейлора по степеням е:
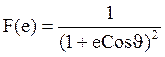
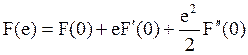
Скорость в любой точке эллиптической траектории можно определить:
![]()
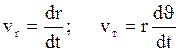
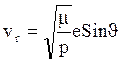
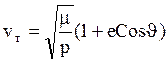
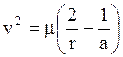 , где а – большая полуось эллипса
, где а – большая полуось эллипса
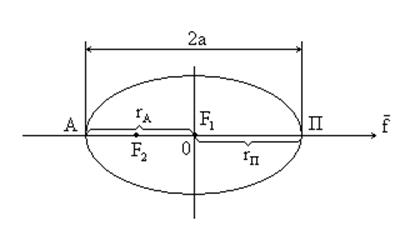
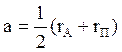
Определение географических координат точки падения по координатам точки конца активного участка и начальным условиям
Для решения этой задачи рассмотрим сферу с
радиусом ![]() , концентричную поверхности Земли:
, концентричную поверхности Земли:
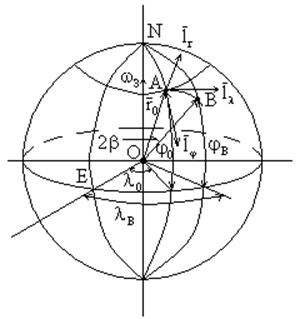
NE – начальный (гринвичский) меридиан
![]() - угловая скорость вращения Земли
- угловая скорость вращения Земли
![]()
Найти: ![]() -
географические координаты точки В (конца активного участка).
-
географические координаты точки В (конца активного участка).
Для решения этой задачи введём с.к. с началом в точке А с
ортами ![]() :
: ![]()
![]() по направлению
по направлению ![]()
![]() по касательной к параллели точки
А
по касательной к параллели точки
А
![]() по касательной к меридиану точки
А
по касательной к меридиану точки
А
Найдём сначала ![]()
![]() ,
, ![]()
![]()
![]()
![]()
Используем следующие условия:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.