Траектории ЛА. Уточнённый метод Эйлера. Расчёт движения по направляющим. Расчёт траектории баллистических ракет и ракет-носителей космических ЛА, страница 7

При Q=const закон изменения массы задаётся m(t)=m0-Qt, где m0 - начальная масса.

 - переменные, при этом выражение сил, входящие в правые части, определены формулами, приведёнными выше.

8 - ое уравнение системы (2) называется программой. Обычно это уравнение представляет из себя кусочно-гладкую кривую. Для всех восьми переменных должны быть заданы начальные значения при t=0.

Запишем систему 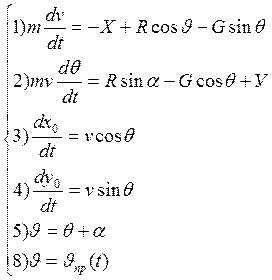(3):

                                                   (3)

  - для этих переменных должны быть заданы начальные условия.

Основным методом расчёта является численное интегрирование. Кроме того, при решении уравнений, может использоваться аналитический метод (метод последовательных приближений (итераций)).

Программная траектория, требования программе, постановка задачи выбора оптимальной программы.

Программа полёта на активном участке в принципе задаётся как одна из зависимостей ,  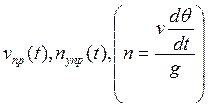или какие-нибудь другие характеристики движения. Программирование может осуществляться не только в вертикальной плоскости Ох0у0, но и в горизонтальной плоскости Ох0z0, а также и для пространственных траекторий. Обычно исходят из программной зависимости , так как угол тангажа  легко измерить с высокой точностью гироскопическими датчиками. Программа задаётся до старта и в процессе движения не корректируется. Особый интерес представляет задача выбора оптимальной программы при решении этой задачи, главными требованиями является получение наибольшей дальности траектории при наименьшем рассеивании точек падения.

14.10.05 *

Задача выбора программы наибольшей дальности может быть решена аналитическими методами классического вариационного исчисления при достаточно грубых допущениях: если считать тягу постоянной, не учитывать силу лобового сопротивления, поле земного тяготения принимать постоянным, параллельным, не учитывать ограничений на углы атаки .

,  - начальное значение угла тангажа

Такая программа предусматривает постоянство угла тангажа на всём активном участке и наклонный старт ракеты. Эта программа не может быть практически реализована.

При выборе программы изменения угла тангажа должны учитываться требования обеспечения достаточного запаса прочности конструкции при наименьшем весе, требования, относящиеся к условиям старта, обеспечение устойчивости движения и т.д., что не было предусмотрено при решении задачи методами классического вариационного исчисления. Выбор программы с учётом всех требований, предъявляемых к ракете, является одним из серьёзных этапов проектирования. Остановимся на этих требованиях и рассмотрим методику выбора программы. Будем рассматривать случай одноступенчатой БР. Вид этого программного уравнения  зависит от назначения ракеты, её конструктивно-технических параметров и вида старта (вертикальный, наклонный). При этом при правильно составленной программе в соответствии с возможностями СУ (ограниченность отклонений управляющих органов) зависимости  должны плавно изменяться, т.е. не иметь угловых точек в процессе полёта на активном участке. Как правило, БР стартуют с ПУ вертикально вверх так, что начальный угол тангажа 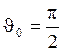 и имеет место начальный вертикальный участок полёта и на некотором интервале времени остаётся таким же. Вертикальный пуск БР позволяет иметь наиболее простые ПУ и обеспечить благоприятные условия для управления на начальном участке траектории. Последнее обстоятельство объясняется тем, что для управления БР, особенно с РДТТ, используется тяга двигателей, часть основной тяги отбирается на управление. Если тяга не достигла своего номинального значения, то будет недостаточна и часть её, используемая для управления. Для выхода двигателя на нормальный режим требуется несколько секунд  и определяет обычно продолжительность начального вертикального участка траектории. Кроме того, вертикальный пуск позволяет снизить требования к жёсткости корпуса БР и, следовательно, уменьшить вес её конструкции.

В интервале .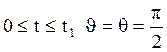

Заметим, что время  должно быть возможно меньшим, т.к. в противном случае увеличиваются потери скорости на преодоление земного тяготения.