Траектории ЛА. Уточнённый метод Эйлера. Расчёт движения по направляющим. Расчёт траектории баллистических ракет и ракет-носителей космических ЛА, страница 4

Физический смысл условий заключается в том, что правая часть является ограниченной. Метод будет иметь смысл только в том случае, если удастся подобрать первую итерацию, достаточно близкую к решению. В этом случае число итераций будет не больше двух или трёх. Для данной задачи удаётся подобрать первую итерацию, близкую к верному решению. Физической основой выбора первой итерации является то, что главной силой в уравнении является тяга.

Первое приближение (итерация). Воспользуемся системой (2’). В первом приближении полагаем , тогда для определения скорости можно использовать уравнение:

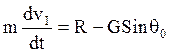
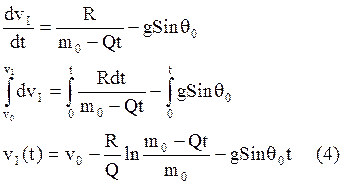
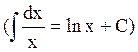
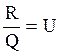 - скорость истечения продуктов сгорания

После определения скорости обращаемся ко второму уравнению системы (2’). Из него находим угол  в первом приближении.

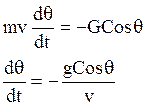
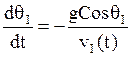 - уравнение с разделяющимися переменными

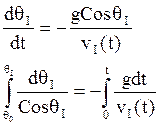
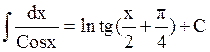
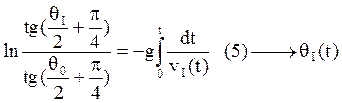
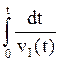- берётся численно по формуле треугольников, трапеций или парабол

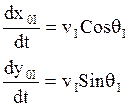
Интегрируя эти уравнения, находим:

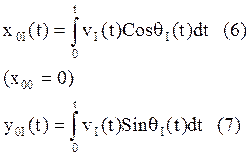
Интегралы берутся численно, на этом первое приближение заканчивается.

Второе приближение основывается на результатах, полученных в первом приближении. Во втором приближении можно учесть силу лобового сопротивления, а также учесть отличие угла  от его значения при сходе с направляющих по результатам первого приближения. А именно, во втором приближении можно учесть силу лобового сопротивления:

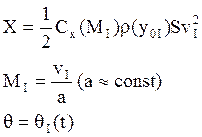
В результате уравнение для определения скорости во втором приближении будет выглядеть следующим образом:

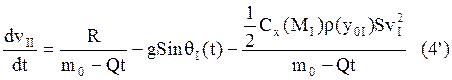
Интегралы берутся численно.

Аналогично угол  во втором приближении находится из уравнения (5’):

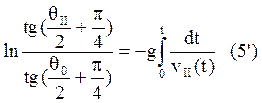
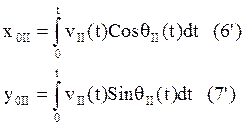
Интегралы берутся численно, на этом второе приближение заканчивается.

Далее можно выполнить третье приближение и т.д. Критерием числа приближений является совпадение с заданной точностью результатов двух следующих друг за другом приближений. Практика расчётов показывает, что достаточно двух приближений.

В результате расчёта определяются параметры движения в конце активного участка

, которые являются исходными данными для расчёта пассивного участка траектории. При расчёте траектории активного участка используются параметры при сходе с направляющих.

Расчёт движения по направляющим.

Будем рассматривать основную задачу, считая направляющую жёсткой, недеформированной. Снаряд принимается за точку. Т.к. скорость мала, то аэродинамическими силами при движении по направляющим можно пренебречь.

23.09.05

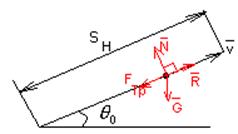
При движении по направляющей пренебрегают аэродинамическими силами, так как  сравнительно мала, зато учитываются реакции по направляющей. Надо учитывать:

Общее уравнение движения:

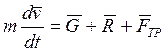                                                                                                     (1)

Sн - длина направляющей;

 - угол наклона;

Рассмотрим два случая:

1)  m=m(t)

;

Q - сек. масс. Расхода;

2)      (не учитывается изменение масс);

R=Qu;

G=mg;

Fтр=fтр*N;

N=G*cos;

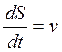                                                                                                                       (2)

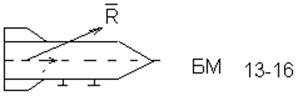
Требуется определить  - скорость схода и время схода tд.

          

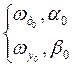
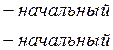
М 13 УК

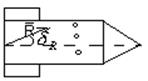
 Сначала рассмотрим первый случай, когда .

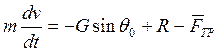, учтем, что Fтр=fтр*N= fтр G*cos и разделим на массу, тогда уравнение запишется так: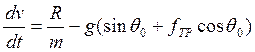

;

;

;

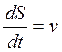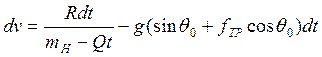Проинтегрируем:

;

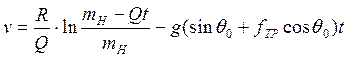                                                               (3)

v=v(t);

;

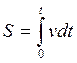Подставляя вместо  её значение, мы получим:

=

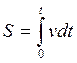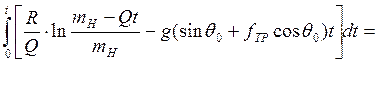
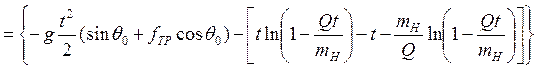                               (4)

S=S(t)

t=tд, S=SH, ;

Это уравнение трансцендентное, оно решается численно. Общий метод можно пояснить следующей схемой:

Введём следующую функцию F(t)= - 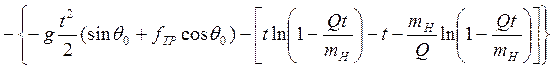и построим график зависимости F(t):

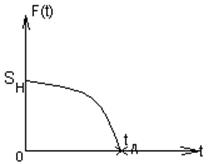
F(tд)=0;

Из уравнения (3) мы находим скорость схода .

Рассмотрим второй случай, когда :

;

,;

 ;

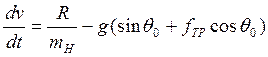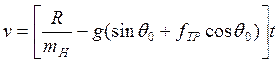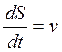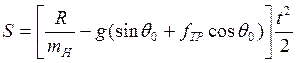Когда S=SH, t=tд, значит из второго уравнения находим tд:

.

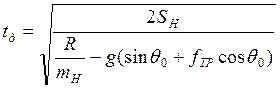
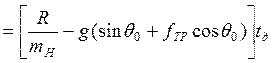Пассивный участок.

Рассмотрим траекторию снаряда ближнего действия.

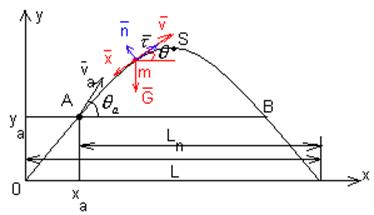
ОА - активный участок;

АSC - пассивный участок;

Исходными данными являются: va, , ,  - параметры конца активного участка.

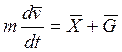                                                                (1)