В главе рассматриваются методы расчёта траектории ЛА, управляемых на активном участке. К таким ЛА относятся, например, баллистические ракеты (БР) и ракеты - носители космических ЛА. Траектория этих ЛА соизмерима с размерами Земли и простирается на большую высоту. Основная часть траектории БР составляет пассивный участок. Дальность полёта БР вдоль поверхности земли, соответствующая активному участку, составляет не более 4-10% общей дальности.
Для существенного увеличения дальности, применяются многоступенчатые БР, которые состоят из отдельных блоков - ступеней, каждая из которых имеет свои двигатели. Идею использования многоступенчатых ракет при освоении космического пространства, впервые предложил К.Э.Циалковский.
Ракеты стартуют с работающей двигательной установки (ДУ) первой ступени. Когда топливо первой ступени израсходуется, включается ДУ второй ступени, а первая ступень отбрасывается. После сброса первой ступени, сила тяги ДУ второй ступени сообщает ускорение меньшей массе, что приводит к значительному увеличению скорости в конце активного участка, по сравнению с одноступенчатыми БР, имеющих одну и туже начальную массу.
Многоступенчатые БР имеют 2-3 ступени. Их стартовый вес составляет несколько десятков тонн, а высота на пусковом участке, при вертикальном старте, около двух десятков метров. Ракеты- носители предназначены для запуска ИСЗ, принципиально не отличаются от континентальных БР. Число их ступеней равно 2-4. Однако ракеты-носители для тяжёлых спутников и космических ЛА, а также для запуска спутников на высокие орбиты или к ЛА на другие небесные тела (луну, планеты) могут быть гораздо крупнее. Их стартовый вес достигает 3000 тонн, а высота на пусковой установке 100 и более метров.
Оперативно - тактические БР с дальностью 300-500 км, как правило, являются одноступенчатыми. Их вес составляет не более 10 тонн, а высота на ПУ при вертикальном старте порядка 10 метров.
Уравнение для расчёта траектории активного участка. Методы расчёта.
Запишем систему уравнений, описывающую управляемый полёт БР на активном участке. Будем рассматривать плоскую задачу и не будем учитывать движение земли, т.е. будем рассматривать идеальную траекторию (не учитывается вращение ракеты около центра масс на движение самого центра масс).
Движение БР на активном участке происходит по задаваемой программной траектории. Расчёт активного участка в зависимости от требуемой точности может производиться как с учётом, так и без учёта кривизны земли. При этом поле земного тяготения принимается центральным, изменяющемся с высотой или соответственно параллельным и постоянным, если не учитывается кривизна траектории.
В отличие от неуправляемых ракет ближнего действия,
в данном случае принципиально учитывается наличие угла атаки ![]() . Ввиду сравнительно большой высоты
активного участка, обычно учитывается зависимость силы тяги от высоты полёта.
. Ввиду сравнительно большой высоты
активного участка, обычно учитывается зависимость силы тяги от высоты полёта.
Рассмотрим текущее положение БР на активном участке в плоскости стрельбы х0у0.
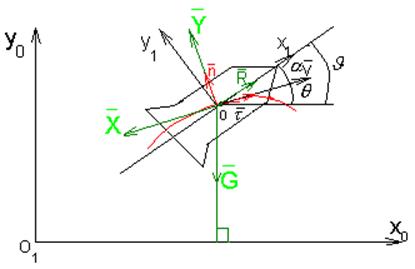
рис.1
G=mg, g=const;
R=R(y0);
R(y0)=Qu +Fвс[Pвс-P(y0)];
Fвс - площадь выходного сечения сопла;
Pвс - давление газа на выходе из сопла;
Q - секундный массовый расход топлива;
u - скорость истечения продуктов сгорания из сопла;
P(y0) - атмосферное давление на высоте y0;
Rз=Qu +Fвс[Pвс-Pз];
Pз - атмосферное давление на уровне земли;
R(y0)= Rз+Fвс[Pз-P(y0)];
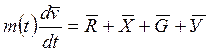 - уравнение Мещерского
(1)
- уравнение Мещерского
(1)
Записав это уравнение (1) в проекциях на выбранные оси координат и добавив обычные кинематические и тригонометрические соотношения, очевидные из рис.1, получили систему уравнений для расчёта траектории активного участка.
![]()
![]()
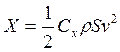 ;
;
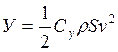 ;
;
![]() ;
;
![]() ;
;
1) Ох0у0
2) ![]()
3) Ох1у1
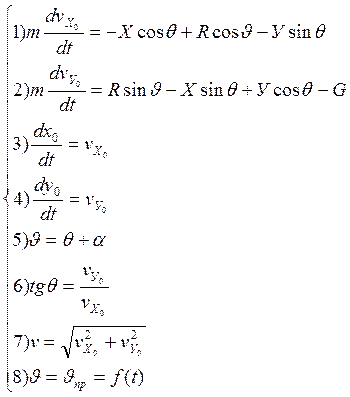 (2)
(2)
Закон изменения массы m(t), плотности ![]() (y0)
и тяги от высоты R(y0) -
известны.
(y0)
и тяги от высоты R(y0) -
известны.
Если закон изменения массы не известен, то добавляется
уравнение 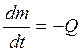 (Q может быть как
переменной, так и постоянной).
(Q может быть как
переменной, так и постоянной).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.