Теперь обратимся к системе (8). Правые части системы (8) соответствуют полностью правым частям (*), тогда можно записать:
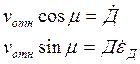 (11)
(11)
![]()
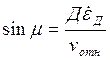
Значение промаха 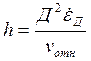 (12)
(12)
Если считать, что ![]()
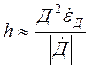
16.12.2005г
При уменьшении расстояния между ракетой и целью, угол ![]() приближается к
приближается к![]() , а
, а ![]() . формулой (13) при малых Д пользоваться нельзя.
Следует также помнить, что входящие в формулу (12) и (13)
. формулой (13) при малых Д пользоваться нельзя.
Следует также помнить, что входящие в формулу (12) и (13) ![]() соответствуют значениям этих величин в
момент прекращения управления. Если не накладывать ограничений на условия
движения ракеты и цели на оставшемся до встречи с целью участке траектории, а
рассматривать наиболее общий случай движения ракеты и цели, движение с
переменной скоростью и маневром. Величина практического промаха будет
отличаться от величины мгновенного промаха, вычисленного по формулам (12) и
(13). Это отличие будет тем существеннее, чем больше расстояние до цели, на
котором было прекращено управления, а также чем больше манёвр и переменность
скоростей ракеты и цели.
соответствуют значениям этих величин в
момент прекращения управления. Если не накладывать ограничений на условия
движения ракеты и цели на оставшемся до встречи с целью участке траектории, а
рассматривать наиболее общий случай движения ракеты и цели, движение с
переменной скоростью и маневром. Величина практического промаха будет
отличаться от величины мгновенного промаха, вычисленного по формулам (12) и
(13). Это отличие будет тем существеннее, чем больше расстояние до цели, на
котором было прекращено управления, а также чем больше манёвр и переменность
скоростей ракеты и цели.
Более точный результат, с учётом манёвра и переменности скоростей, может быть получен, если предположить, что с момента выключения управления, движение ракеты и цели происходит с постоянной осевой и нормальной перегрузками. Промах ракеты, рассчитанный при таких допущениях, будем называть фактическим промахом. (Кринетский Е.И. Системы наведения, 70г).
Можно показать, что при дальностях выключения управления, соответствующим дальностям «ослепления» головки самонаведения, допущения о постоянстве маневра ракеты и цели на оставшемся до встречи участке траектории не является грубым. При указанных допущениях приведём формулу для определения величины фактического промаха ракеты.
Примем во внимание, что дальность до встречи ракеты с целью и кривизна траектории не очень велики. Тогда имеет место следующая формула:
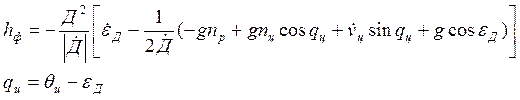 (14)
(14)
![]() - составляющая перегрузки ракеты
по нормали к линии визирования (линии Ракета-Цель);
- составляющая перегрузки ракеты
по нормали к линии визирования (линии Ракета-Цель);
g=9,81 м/![]() ;
;
![]() - нормальное к линии визирования
составляющая перегрузки, обусловленная весом ракеты.
- нормальное к линии визирования
составляющая перегрузки, обусловленная весом ракеты.
Метод наведения трёхточечного типа.
Выше было отмечено, что эти методы реализуются при
телеуправлении. Как и в предыдущем параграфе будем рассматривать движение
ракеты и цели в вертикальной плоскости ![]() .
.
Взаимное положение ракеты и цели в вертикальной плоскости показано на рис.1:
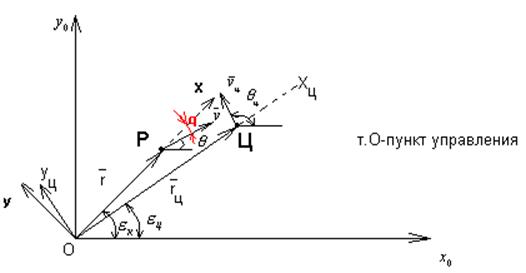
Для современных методов наведения q=(5-10![]() ). Общий вид уравнения, определяющий
любой метод наведения трёхточечного типа, в случае плоского движения ракеты и
цели можно представить следующей формулой:
). Общий вид уравнения, определяющий
любой метод наведения трёхточечного типа, в случае плоского движения ракеты и
цели можно представить следующей формулой:
![]() (1)
(1)
![]()
Из уравнения (1) видно, что оно удовлетворяет основным требованиям, предъявляемым к методу наведения.
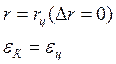
А(t) - коэффициент, определяющий свойство метода наведения. Этот коэффициент может быть переменным, зависящим от координат и параметров движения, или в частном случае, постоянным в течении всего времени полёта ракеты до цели.
Конкретизируем уравнение (1) для различных методов наведения трёхточечного тип. Как было указано выше, наиболее распространёнными методами наведения являются:
Метод «накрытия» цели (метод совмещения трёх точек) и спрямляющие методы.
1)Метод «накрытия» цели
А(t)![]() (2)
(2)
![]()
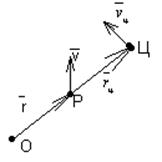
Три точки - О, Р и Ц - во всё время движения находятся на одной линии.
2)Метод спрямления траектории (спрямляющие методы)
Выбором коэффициента А(t) можно
свести к нулю угловую скорость радиуса - вектора текущей точки кинематической
траектории в районе встречи с целью, не предъявляя особых требований к её
величине на других участках кинематической траектории. Это означает, что в
районе точки встречи с целью, кинематическая траектория ракеты должна быть касательной
к линии визирования цели, которая определяется направлением вектора ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.