Траектории ЛА. Уточнённый метод Эйлера. Расчёт движения по направляющим. Расчёт траектории баллистических ракет и ракет-носителей космических ЛА, страница 2

Математическая постановка задачи расчёта траектории.

Движение ЛА описывается известной системой дифференциальных уравнений. В векторной форме уравнения пространственного движения можно записать в виде:

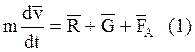
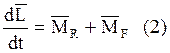
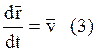
m=m(t), где  - момент количества движения,  - момент тяги,  - момент остальных сил,

 - абсолютная угловая скорость вращения относительно ц.м.

(1) – уравнение Мещерского

(2) – векторное уравнение вращательного движения ц.м.

(3), (4) – кинематические соотношения

На пассивном участке , , .

При

(5) – начальные условия

Интегрирование системы выполняется на интервале , заданном или определяемом конечным условием. При исследовании управляемого движения следует задать уравнения СУ, которые определяются следующим функциональным соотношением:

(1) – (6) – система является замкнутой и определяет единственную траекторию ЛА

При расчёте траектории от векторных уравнений следует перейти к скалярным уравнениям, используя с.к., рассмотренную в первой части курса. На первых этапах можно не учитывать влияние вращательного движения на траекторию. При этом ЛА можно рассматривать как материальную точку и использовать следующую векторную систему:

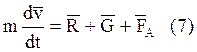
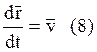
В общем случае задача расчёта траектории ЛА может быть сформулирована как задача интегрирования замкнутой системы дифференциальных уравнений:

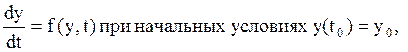где y – конечно-мерный вектор фазовых координат,  t – время,  - известная вектор-функция,  - заданные начальные условия. Момент окончания интегрирования может быть задан интервалом  или определяется функциональным соотношением . Основным методом расчёта является метод численного интегрирования, однако, существуют и приближённые аналитические методы расчёта.

Алгоритмы некоторых методов численного интегрирования

дифференциальных уравнений

Пусть задано одно дифференциальное уравнение, записанное в нормальной форме Коши:

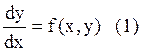
и заданы начальные условия:

Требуется найти решение уравнения (1), удовлетворяющее начальным условиям (2). На геометрическом языке найти (построить) интегральную кривую уравнения (1), проходящую через заданную начальную точку (2). Эта задача называется задачей Коши для уравнения (1). Будем считать, что задача Коши для уравнения (1) имеет единственное решение. Основная идея численного интегрирования заключается в замене (аппроксимации) искомой интегральной кривой полиномом. Решение получается в виде таблицы искомых значений функции для значений аргумента, отличающихся друг от друга на шаг. Запишем уравнение (1) в интегральной форме:

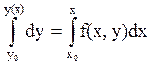
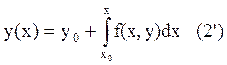
Зададим h>0 – шаг интегрирования, тогда

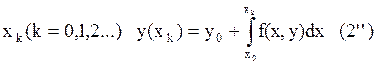
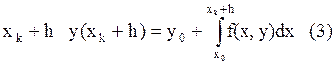
С учётом (2’), (3)-(2’’):

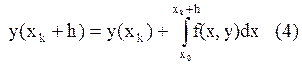
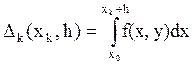
Т. о., получили связь между значениями искомой функции при значениях аргумента, отличающихся на шаг. Эта связь выражается через функцию . Различные методы численного интегрирования отличаются теми аппроксимациями f(x,y), которые используются при вычислении . Наиболее известны следующие методы численного интегрирования:

1) метод Эйлера;

2) метод Рунге-Кутта;

3) метод Адамса-Штермера.

Метод Эйлера.

В методе Эйлера принимается следующий алгоритм:

                      

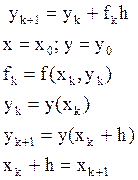
x	y
…	…

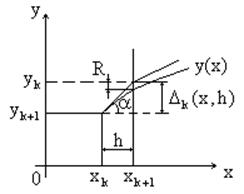
Геометрический смысл

,  

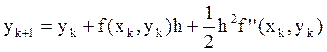
В методе Эйлера истинная интегральная кривая заменяется ломаной линией, угловые координаты сторон которой  определяются по начальной точке каждого шага. Если выбрать h маленький, а интегральная кривая плавная, то метод Эйлера может дать приемлемый результат по точности. Теория даёт следующий порядок ошибки на одном шаге .

9.09.05

Уточнённый  метод Эйлера.

В этом методе истинная интегральная кривая также заменяется локальной, однако угловой коэффициент сторон этой ломанной определяется не по начальной точке шага, а выбирается некоторым средним значением углового коэффициента начальной и конечной точки шага. Но так как конечная точка шага не известна, то организуется итерационный процесс для определения этой конечной точки.