Траектории ЛА. Уточнённый метод Эйлера. Расчёт движения по направляющим. Расчёт траектории баллистических ракет и ракет-носителей космических ЛА, страница 22

23.12.05 *

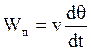
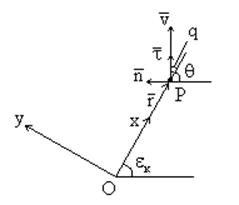
Т.к. q – маленький угол, то  - трансверсальная составляющая полного ускорения

1) Метод накрытия цели (метод совмещения трёх точек)

                (1)

 характеризует влияние скорости движения цели на величину нормального ускорения ракеты на кинематической траектории.

 характеризует влияние манёвра цели на величину .

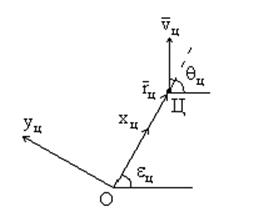
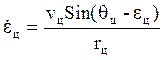
Если цель высокоскоростная (большое ) и высокоманевренная (большое ), то в методе накрытия получим значительное нормальное ускорение на кинематической траектории. Значит можно сделать вывод, что метод накрытия цели с точки зрения критерия  эффективен для малоскоростных и маломаневренных целей.

2) Спрямляющие методы.

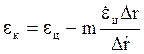
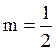 - метод половинного спрямления

 - метод полного спрямления

Получим следующее выражение:

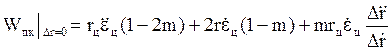
Последнее слагаемое мало и для оценки качества метода им можно пренебречь.

При m=1 пропадает второе слагаемое, которое содержит .

При 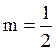 пропадает первое слагаемое, которое содержит .

Т.о. можно сделать вывод:

Метод полного спрямления более эффективен для поражения высокоскоростных ( пропадает), но маломанёвренных целей ( остаётся).

Метод половинного спрямления более эффективен для поражения высокоманевренных ( пропадает), но малоскоростных целей ( остаётся).

 (задаётся заранее программой)

С точки зрения этого критерия получаем:

Устройство выработки команды управления:

1) метод накрытия цели

(задаётся заранее программой)х целейивен для поражения высокоскоростных иятической траектории. тической траекториию

2) спрямляющие методы

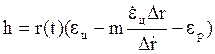
Уравнения для расчёта кинематических траекторий

Для вывода уравнений для расчёта кинематических траекторий аналогично тому, как мы делали ранее для методов наведения двухточечного типа, получим основное кинематическое соотношение методов наведения трёхточечного типа.

1)

2)

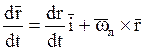, где

- абсолютная угловая скорость радиус-вектора

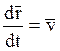
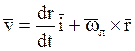                    (1)

(1) – основное кинематическое соотношение методов наведения трёхточечного типа

Для цели аналогично можно записать:

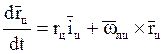
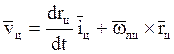
Для случая плоского движения , - орт оси

Используя уравнение (1) и представление  для плоского движения, запишем уравнение (1) в проекциях на оси х и у.

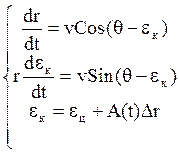                       (2)

Если считать, что известно , , , то система (2) служит для определения трёх переменных величин .

При произвольном движении цели в плоскости система решается численным интегрированием. Возможен частный случай, когда удаётся получить аналитическое решение: если .

Для быстрых расчётов кинематической траектории ракеты при наведении по методу накрытия цели используется следующий способ.

Движение и скорость движения цели известны:

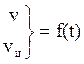
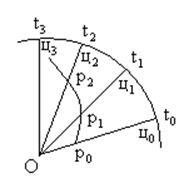
Получим положение ракеты в момент времени . Для этого из точки  радиусом 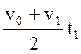 делаем засечку на прямой , получаем положение ракеты . Для того чтобы получить положение ракеты в момент времени  из точки  радиусом 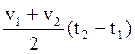 делаем засечку на прямой , получаем положение ракеты  и т.д.

Интервал времени  должен быть малым с тем, чтобы иметь основание среднюю скорость ракеты на этом интервале вычислять по формуле 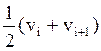. Чем меньше отношение , тем больше окажется кривизна кинематической траектории.

В более общем случае скорость ракеты  может быть заранее неизвестна. Запишем систему уравнений для определения траектории ракеты для произвольного метода телеуправления, если задано движение цели.

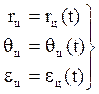 - заданы, но неизвестно, тогда

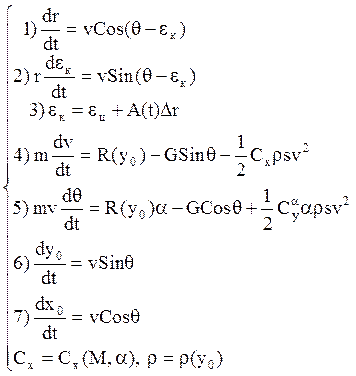                       (3)

Переменные: .

Задача может быть решена только методами численного интегрирования. Пятое уравнение служит для определения угла атаки . Если по каким-либо соображениям удаётся осреднить угол атаки  и положить, тогда из этой системы можно выбросить пятое уравнение.