Траектории ЛА. Уточнённый метод Эйлера. Расчёт движения по направляющим. Расчёт траектории баллистических ракет и ракет-носителей космических ЛА, страница 5

Система уравнений для расчёта пассивного участка будет иметь такой же вид, как для активного участка.

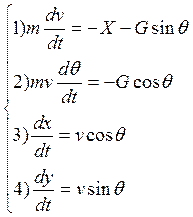                                              (2)

m=const;

;

;

Начальные условия, при которых надо интегрировать систему (2):

t=0 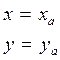 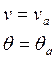                                          (3)

Система решается методом численного интегрирования. Расчёт заключается в тот момент, когда у в точке С равно нулю (т.е. ).

Запишем систему уравнений при аргументе х для расчёта пассивного участка.

Для этого каждое из уравнений разделим на третье уравнение:

  

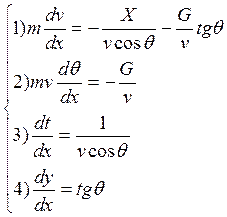
Систему можно записать в нормальной форме Коши:

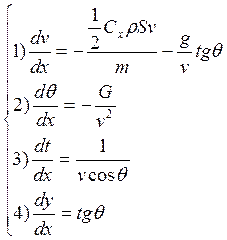
Когда  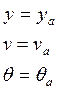      - начальные условия.

Однако при решении некоторых задач могут быть использованы артиллерийские баллистические таблицы.

Использование артиллерийских баллистических таблиц.

Эти таблицы приспособлены (используются) для расчёта траектории артиллерийского снаряда, точки вылета и падения которого находятся на земле на одной высоте. Эти таблицы построены численным интегрированием уравнений движения артиллерийского снаряда при следующих начальных условиях:

t=0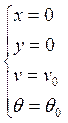          

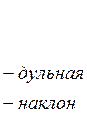
Входными данными являются: v0, ,  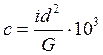- баллистический коэффициент, где    d - калибр [м];

i - коэффициент формы (i=);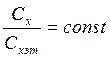

G - [кг];

АБР могут быть использованы для расчёта участка АВ, где В - точка на высоте, одинаковой с точкой А, при этом входными данными в АБТ являются:

   

 - приведенный баллистический коэффициент;

 ,  у_а - [м], 

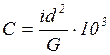
30.09.05 *

Для расчёта участка BC помимо метода численного интегрирования можно использовать приближённый аналитический метод.

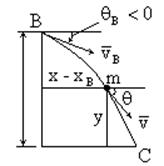
Приближённый аналитический метод основан на использовании разложения основных элементов траектории в ряд Тейлора произвольной точки в окрестности точки B.

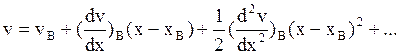
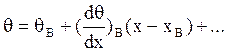
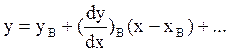
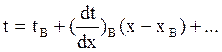
Производные вычисляются на основании системы уравнений (4) на пассивном участке при аргументе х.

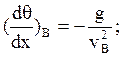
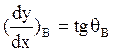 и т.д.

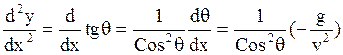
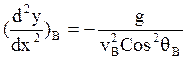
Геометрический смысл этого метода заключается в том, что траектория на участке BC апроксимируется параболой.

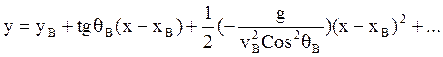
Если сохраним первые два слагаемых, то получится уравнение прямой.

Параметры точки С определяются следующим образом:

Полагаем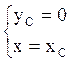

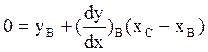
Подставляя  в другие уравнения, мы найдём:

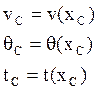
Если высота  достаточно велика, то для расчёта траектории могут использоваться таблицы для бомбометания с пикированием.

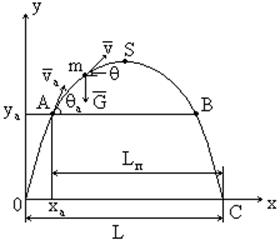
Параболическая теория.

Параболическая теория изучает движение тяжёлой материальной точки с постоянной массой в пустоте в однородном параллельном поле земного тяготения. Результаты этой теории используются для расчёта пассивного участка реактивных снарядов, если можно пренебречь аэродинамическими силами. Кроме того, выводы параболической теории используются для определения параметров активного участка.

 - полная дальность

 - дальность пассивная

 - дальность активная

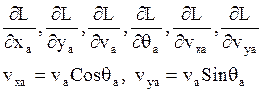
Знание этих коэффициентов необходимо для определения рассеивания точки падения в зависимости от отклонения параметров конца активного участка.

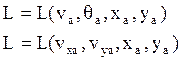
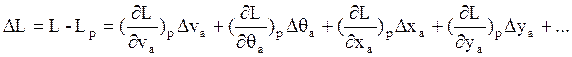 - разложение Тейлора функции L в окрестности расчётной траектории

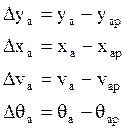
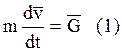
Это уравнение запишем в проекциях на оси x и y с.к. 0xy:

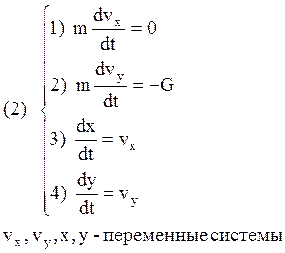
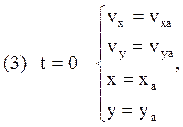 где индексом а обозначены параметры конца активного участка

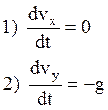
Интегрируя первое уравнение, получим .

Интегрируя второе уравнение, получим .

Обращаемся к третьему и четвёртому уравнениям:

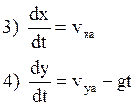
Интегрируя эти уравнения при заданных начальных условиях, получаем:

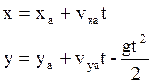
Параметрические уравнения траектории в условиях допущений параболической теории.

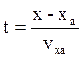
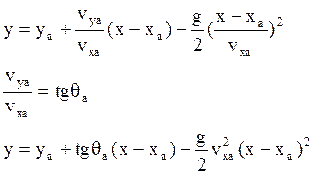
На основании полученных соотношений можно определить параметры любой точки траектории. Найдём параметры траектории в точке С. Обозначим:

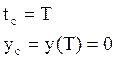
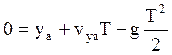
Решая это квадратное уравнение, получаем:

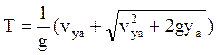
Подставляя это значение Т в выражение для х, найдём полную дальность:

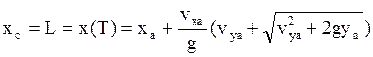
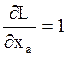
Самостоятельно определить:

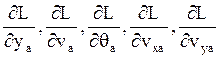
Найдём скорость и угол в точке  С:

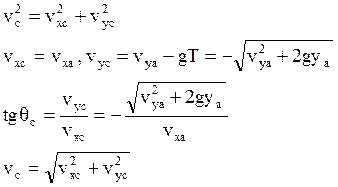
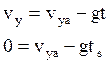
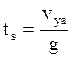
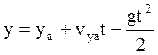
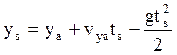
Подставляем:

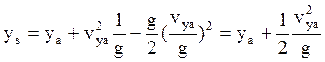
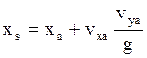
07.10.2005г

Глава 2.

Расчёт траектории баллистических ракет и ракет - носителей космических ЛА.

Введение.