![]() (7)
(7)
![]() - орт вектора r (
- орт вектора r (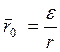 );
);
![]() - вектор Лапласа, это вектор,
проекции которого
- вектор Лапласа, это вектор,
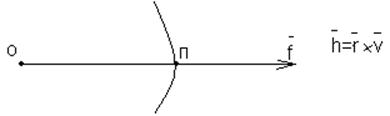
проекции которого ![]() . Вектор Лапласа лежит абсолютной
плоскости стрельбы (плоскости, проходящей через
. Вектор Лапласа лежит абсолютной
плоскости стрельбы (плоскости, проходящей через ![]() и
и ![]() ), и направлен в точку, ближайшую к
притягивающему центру (точка п)) - периметр орбиты.
), и направлен в точку, ближайшую к
притягивающему центру (точка п)) - периметр орбиты.
Интеграл Лапласа можно записать в проекциях на оси инерциальной системы координат, при этом мы будем учитывать:
![]()
![]()
![]()
 (8)
(8)
Таким образом, мы получили семь скалярных первых интегралов
и соответственно семь постоянных: ![]() ,
,![]() и
H.
и
H.
Однако семь первых интегралов (3), (6) и (8) не могут составить решение уравнений (2), так как:
1) не один из них не содержит явно времени;
2) имеет место два тождественных соотношения:
1 - ое соотношение имеет
простой геометрический смысл -![]() (9)
(9)
2 - ое соотношение имеет следующий физический смысл:
![]() (10)
(10)
Из соотношения (10) следует, что модули векторов f, H и h не могут быть одновременно равны нулю. Из соотношения (9) и (10) можно выразить любые две из семи постоянных функции пяти остальных, которые остаются произвольными. Таким образом, оказывается, что независимых первых интегралов - пять, а система у нас шестого порядка, значит должны быть шесть первых интегралов. Можно показать, что недостающий шестой интеграл и соответственно шестую независимую постоянную можно получить простой квадратурой. Смотрите, например, книгу Иванов Н.М., Лысенко Л.Н. Баллистические и навигационные космические аппараты.
И, следовательно, общее решение системы (2) в виде зависимости
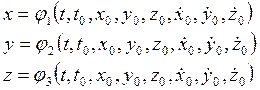 (11)
(11)
может быть получено принципиально. Однако, реализация этой процедуры затруднительна, так как уравнения для первых интегралов являются уравнениями второй степени относительно независимых координат и содержат иррациональность, представляемую радиусом - вектором. К некоторому упрощению приводит использование выявленных ранее свойств.
Ранее было показано, что траектория невозмущённого движения лежит в плоскости, уравнение которой представляется формулой (4), то есть является плоской кривой. Чтобы определить вид и расположение этой кривой надо иметь второе уравнение, содержащее координаты. Это уравнение находят из интегралов Лапласа (7) и (8).
Используем выражение (7). Умножим (7) скалярно слева и справа на r, то есть:
![]()
![]()
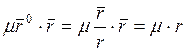
![]() или, выражая через проекции,
получим:
или, выражая через проекции,
получим:
![]() (12)
(12)
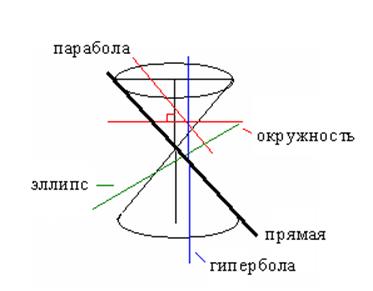
Уравнение (12) содержит координаты x, y, z и представляет собой уравнение некоторой поверхности вращении (конической), на которой остаётся ЛА в процессе своего движения. В силу этого уравнение (4) и (12) определяют уравнение траектории ЛА. Эта траектория представляет собой линию пересечения плоскости (4) и поверхности (12). Эта линия представляет собой кривую второго порядка, которая называется кривой конического сечения, которая может быть окружностью, эллипсом, параболой или гиперболой, или в вырожденном случае парой прямых, в зависимости от взаимного расположения плоскости (4) и поверхности (12).
Так как траектория является плоской кривой, то
целесообразно от инерциальной системы координат Oxyz
перейти к новой системе координат ![]() , взяв плоскость орбиты
за основную плоскость (
, взяв плоскость орбиты
за основную плоскость (![]() ),
),![]() перпендикулярно
плоскости орбиты, то есть перпендикулярно вектору
перпендикулярно
плоскости орбиты, то есть перпендикулярно вектору ![]() , то
есть рассмотрим вот эту плоскость.
, то
есть рассмотрим вот эту плоскость.
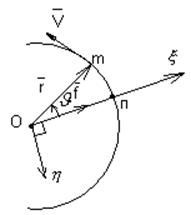
В плоскости ![]() введём
полярные координаты
введём
полярные координаты ![]() .
.
![]() - греческая буква ипсилон;
- греческая буква ипсилон;
Причём полярную ось выберем по направлению вектора Лапласа.
Используя выражение ![]() и учитывая, что радиус - вектор
отсчитывается
и учитывая, что радиус - вектор
отсчитывается ![]()
![]() .
.
Из последнего выражения получаем уравнение траектории в полярных координатах.
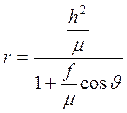 ;
;
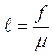 - эксцентриситет;
- эксцентриситет;
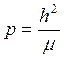 - фокальный параметр;
- фокальный параметр;
Тогда получим: 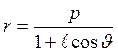 (13)
- уравнение кривой конического сечения, фокус которого находится в
притягивающем центре, а притягивающая ось является осью симметрии.
(13)
- уравнение кривой конического сечения, фокус которого находится в
притягивающем центре, а притягивающая ось является осью симметрии.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.