Траектории ЛА. Уточнённый метод Эйлера. Расчёт движения по направляющим. Расчёт траектории баллистических ракет и ракет-носителей космических ЛА, страница 15

Задача управления дальностью БР. Функционал управления дальностью.

В процессе полёта на ракету действуют различные возмущающие факторы, которые приводят к отклонению действительной траектории от идеальной. Возмущающие факторы могут иметь случайный характер или быть детерминированными. Так, в частности, отклонения аэродинамических коэффициентов от их расчётных значений носят (имеют) в основном детерминированный характер, а отклонение удельной тяги двигателя носит случайный характер и так далее. Обратимся к траектории БР.

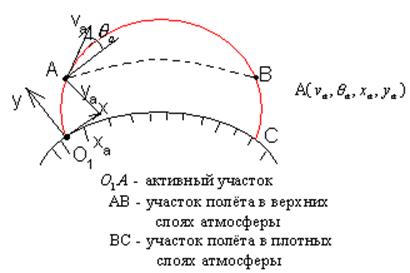
Наиболее существенное влияние на рассеивание точек падения оказывает активный участок траектории О1А и практически не влияет участок АВ. На участке ВС в плотных слоях атмосферы, на ракету действует  сопротивление воздуха и сила тяжести. В верхней части этого участка ракета движется с большими углами атаки, разброс которых приводит к рассеиванию точек падения. Кроме того, на этом участке имеют место отклонения параметров атмосферы от расчётных. Это также является причиной рассеивания ракеты. Однако ракета проходит участок ВС за сравнительно короткое время, поэтому отклонения координат не успевают достичь больших значений, поэтому участок ВС оказывает значительно меньшее влияние на рассеивание, чем активный участок О1А.

Это показывает, что для уменьшения рассеивания ракеты, нужно в первую очередь бороться с влиянием возмущения, которые действуют на активном участке. БР чаще всего управляется только на активном участке О1А, на участке ВС может производиться импульсная коррекция траектории. Участок АВ, расположенный в разряжённых слоях атмосферы, оказывается неуправляемым. Рассмотрим задачу управления дальностью полёта БР, управляемой на активном участке.

02.12.05 *

Будем считать, что полная дальность полёта БР определяется значениями параметров продольного движения в конце активного участка и не зависит от параметров бокового движения.

Будем считать, что эти отклонения – малые величины.

Разложим функцию L в ряд Тейлора в окрестности расчётного движения и будем учитывать члены разложения, содержащие отклонения параметров от расчётного движения, в степени не выше первой:

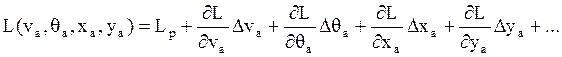                 (1)

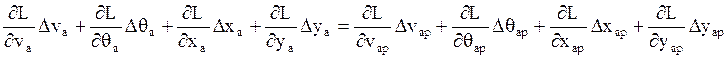Частные производные, входящие в уравнение (1), являются функциями тех же параметров в расчётном движении и для выбранного расчётного движения являются постоянными величинами. Для того чтобы отклонение по дальности , необходимо, чтобы выполнялось условие (2):

    (2)

Введём в рассмотрение некоторую функцию :

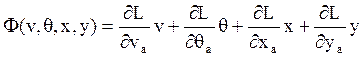
Тогда условие (2) (отсутствие отклонений по дальности в конце траектории) может быть записано в следующем виде:

                   (3)

(3) – уравнение управления дальностью

называется управляющей функцией или функционалом управления дальностью, т.о., чтобы отклонение по дальности БР, управляемой на активном участке, равнялось нулю, необходимо в полёте на активном участке непрерывно или достаточно часто изменять величины , вычислять управляющую функцию Ф и сравнивать её с рассчитанным для данной дальности значением . В момент времени, когда текущее значение управляющей функции Ф сравнивается с её расчётным значением, производится отсечка тяги двигателя (конец активного участка). Управляющую функцию можно упростить, если на участке отсечки тяги угол  обеспечивать равным углу наибольшей дальности, то 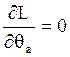 и одно слагаемое в формуле для Ф пропадает.

А.Ю. Ишлинский в книге «Инерциальное управление БР» разработал теорию, которая позволяет найти такое положение измерительных осей акселерометров, при которых отклонение одного из параметров движения в конце активного участка перестаёт влиять на дальность полёта («» и «» направления).

Следует отметить, что даже точная реализация условия (3) не устраняет отклонение по дальности по следующим причинам:

1) не учтены квадратичные члены в разложении для управляющей функции;