11) ![]() (обозначение десятичного логарифма)
(обозначение десятичного логарифма)
Графики логарифмических функций можно
получить из графиков показательных функций с тем же основанием ![]() путем отражения относительно прямой
путем отражения относительно прямой ![]() (см. рис. 8). Область определения
логарифмических функций
(см. рис. 8). Область определения
логарифмических функций ![]() . При
. При ![]() логарифмические функции возрастают, при
логарифмические функции возрастают, при ![]() - убывают.
- убывают.
Определение 7: К тригонометрическим функциям относят следующие функции:
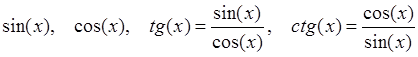 ,
(41)
,
(41)
где ![]() и
и ![]() определяются
как декартовы координаты точки с полярными координатами
определяются
как декартовы координаты точки с полярными координатами ![]() (точки
на единичной окружности, см. рис. 9а), или, в случае комплексного
(точки
на единичной окружности, см. рис. 9а), или, в случае комплексного ![]() , по формулам Эйлера (14).
, по формулам Эйлера (14).
Основные свойства тригонометрических функций:
1)
![]() (основное тригонометрическое
тождество)
(основное тригонометрическое
тождество)
2)
![]() (нечетность функции синуса)
(нечетность функции синуса)
3)
![]() (четность функции косинуса)
(четность функции косинуса)
4)
![]() (график
(график ![]() получается
путем сдвига графика
получается
путем сдвига графика ![]() влево на
влево на ![]() )
)
5) ![]() 6)
6)
![]()
7) ![]() 8)
8)
![]()
9)
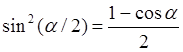 10)
10) 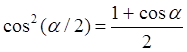
11) ![]() 12)
12) ![]()
13) ![]() 14)
14)
![]()
15)
![]()
Все вышеперечисленные свойства легко доказать на основе формул Эйлера (14).
Пример 1: Вывести формулы 7) и 13).
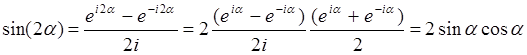
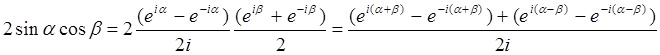
![]()
Полезно запомнить значения ![]() и
и ![]() для
аргументов
для
аргументов ![]() , кратных
, кратных ![]() и
и ![]() (см. рис. 9б). Графики тригонометрических
функций приведены на рис. 10, 11.
(см. рис. 9б). Графики тригонометрических
функций приведены на рис. 10, 11.
![]() ;
;
![]() ;
; ![]()
Определение 8: Функцию, представленную в виде
![]() ,
(42)
,
(42)
будем называть осциллирующей функцией с амплитудой
![]() , циклической частотой
, циклической частотой ![]()
![]() и начальной фазой
и начальной фазой
![]() .
.
Определение 9: К обратным тригонометрическим функциям относят функции
![]() (43)
(43)
которые удовлетворяют определяющему свойству всех обратных функций:
![]() (44)
(44)
![]()
![]()
Поскольку тригонометрические
функции не являются монотонными во всей области определения, обратные
тригонометрические функции многозначны. Под ![]()
![]()
![]() и
и ![]() обычно понимают главные значения
обратных тригонометрических функций, которые, в соответствии с интервалами
монотонности тригонометрических функций, определяются следующими формулами:
обычно понимают главные значения
обратных тригонометрических функций, которые, в соответствии с интервалами
монотонности тригонометрических функций, определяются следующими формулами:
1)
![]()
![]()
![]()
2)
![]()
![]()
![]() (45)
(45)
3)
![]()
![]()
![]()
4)
![]()
![]()
![]() .
.
Главные значения обратных тригонометрических функций удовлетворяют двум дополнительным свойствам:
![]() (46)
(46)
![]() (47)
(47)
Пример 2: Вычислить ![]() .
.
![]()
Графики обратных тригонометрических функций
приведены на рис. 12, 13. Функции ![]() и
и ![]() являются нечетными, функции
являются нечетными, функции ![]() и
и ![]() четностью
не обладают.
четностью
не обладают.
9. Числовая последовательность. Предел последовательности
Определение 1: Последовательностью называют всякую функцию,
определенную на множестве натуральных чисел ![]() .
.
Как правило, последовательность задается одним из
двух способов: заданием формулы для ![]() - го
члена последовательности
- го
члена последовательности
![]() где
где
![]() - некоторая известная функция,
- некоторая известная функция, ![]() , или заданием рекуррентного соотношения, то есть
указанием нескольких первых членов последовательности и правила, на основании
которого каждый последующий член последовательности может быть определен по
значениям предыдущих.
, или заданием рекуррентного соотношения, то есть
указанием нескольких первых членов последовательности и правила, на основании
которого каждый последующий член последовательности может быть определен по
значениям предыдущих.
Пример 1: Геометрическая прогрессия со знаменателем ![]()
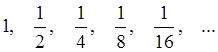
может быть задана формулой для ![]() - го
члена
- го
члена 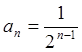 , или же рекуррентным соотношением
, или же рекуррентным соотношением ![]() .
.
Основной характеристикой последовательности
является предел последовательности, то есть число, к которому
приближается ![]() по мере увеличения
по мере увеличения ![]() .
.
Определение 2: Говорят, что последовательность ![]() имеет
предел, равный
имеет
предел, равный ![]() , если для любого (сколь угодно
малого)
, если для любого (сколь угодно
малого) ![]() можно указать
можно указать ![]() , такое
что для всякого
, такое
что для всякого ![]() выполняется неравенство
выполняется неравенство ![]() . Пишут
. Пишут
![]() или
или ![]() . (48)
. (48)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.