Математический анализ функции одной переменной: Учебное пособие. Часть 1 (Элементы математической логики. Множества чисел. Комплексные числа. Производная функции. Дифференциал), страница 6

Наиболее полным с точки зрения математического анализа является аналитический способ задания функции, то есть задание ее в виде формулы. Функция, заданная в виде  называется явно заданной функцией. Функция, заданная в виде  называется неявно заданной функцией.

Помимо аналитического способа используют табличный и графический способы задания функции. Табличный способ является наименее информативным: по сути дела он определяет функцию только для нескольких точек , при этом значения функции между точками  остаются неизвестными. Для оценки значений функции  между табличными точками  необходимо иметь дополнительную информацию о гладкости функции (об отсутствии резких изменений функции между точками ).

Графический способ является более информативным и максимально наглядным, однако же, он задает значения функции  только приближенно (с точностью, не превосходящей, например, толщину линии графика).

Пример 1: Дана таблица значений функции:

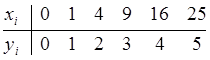
Построить график функции, проходящей через заданные точки.

Нетрудно заметить, что функция  удовлетворяет всем табличным точкам. Помимо нее, существует бесконечное множество других функций, также удовлетворяющих всем табличным точкам. Например: , где  для всех , или же , где  для всех . На рис. 2 изображены графики трех функций:   , каждая из которых удовлетворяет приведенной таблице, при этом функция  является наиболее гладкой и, следовательно, наиболее подходит для аппроксимации табличных значений. Для задания функций  и  необходима таблица значений с более частым расположением точек .

Определение 2: Множество чисел , для которых определено правило сопоставления  называют областью определения функции (ООФ). Иначе говоря, если для заданного  возможно определить (вычислить) , то  принадлежит ООФ.

            Следует отметить, что функция, изначально определенная в области , может быть впоследствии расширена на область , то есть дополнительно определена для , при этом для всех  значения расширенной функции совпадают со значениями исходной. Если расширенная функция оказывается при этом гладкой (непрерывна функция и все ее производные) во всей области , то говорят, что имеет место аналитическое продолжение исходной функции из области  в область .

Пример 2: Функция, заданная таблицей значений из примера 1, имеет область определения, состоящую и шести целых чисел: . Как было показано в примере 1, можно предложить различные варианты расширения данной функции на часть вещественной оси. В частности, приведенные функции  являются аналитическими продолжениями исходной функции в область . В области  все три указанные функции вещественны. Если определить корень из комплексного числа формулой  или же формулой   , мы получим для каждой из функций  одно из двух возможных аналитических продолжений (двух ветвей) на множество всех комплексных чисел , при этом областью определения функций становится вся комплексная плоскость.

            В дальнейшем под ООФ мы будем понимать множество всех вещественных , для которых значения функции вещественны.  

Определение 3: Множеством значений функции (МЗФ) называют множество всех  где ООФ.

Пример 3: Определить множество значений для каждой из функций .

:  (положительная вещественная полуось)

:  (вся вещественная ось)

Действительно, поскольку амплитуда осциллирующего слагаемого  растет быстрее, чем , минимумы функции  будут становиться все более отрицательными по мере увеличения  ( уменьшается с ростом  при больших ).

:

Определение 4: Функция  называется неубывающей (невозрастающей) на интервале , если для любых  верно утверждение    ( для невозрастающих функций). Неубывающие и невозрастающие функции называют монотонными.

Определение 5: Функция  называется возрастающей (убывающей) на интервале , если для любых  верно утверждение    ( для убывающих функций). Возрастающие и убывающие функции называют строго монотонными.