Пример 4: Исследовать сходимость ряда 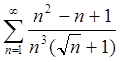 .
.
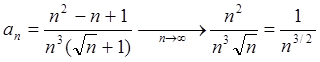 . Поскольку ряд
. Поскольку ряд ![]() , где
, где 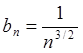 сходится,
а
сходится,
а  , то согласно признаку сравнения 1.2 ряд
, то согласно признаку сравнения 1.2 ряд ![]() также является сходящимся.
также является сходящимся.
Пример 5: Исследовать сходимость ряда ![]() (смотри (5))
(смотри (5))
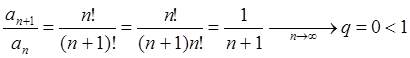 , следовательно, согласно
признаку Даламбера, ряд сходится.
, следовательно, согласно
признаку Даламбера, ряд сходится.
Определение 4: Ряд вида
![]() ,
(56)
,
(56)
где все ![]() (либо все
(либо все ![]() ) называют знакочередующимся.
) называют знакочередующимся.
Достаточное условие (признак) сходимости знакочередующегося ряда можно сформулировать в следующем виде.
Теорема 2 (Лейбница): Знакочередующийся ряд ![]()
![]() сходится, если
сходится, если
1) ![]() (необходимое условие)
(необходимое условие)
2) Начиная с
некоторого ![]() выполняется неравенство
выполняется неравенство ![]() (последовательность абсолютных значений
членов ряда не возрастает).
(последовательность абсолютных значений
членов ряда не возрастает).
Действительно, как видно из примера на рис. 16,
последовательность частичных сумм ![]() такого ряда является
ограниченной и осциллирует с амплитудой, стремящейся к нулю (поскольку
такого ряда является
ограниченной и осциллирует с амплитудой, стремящейся к нулю (поскольку ![]() ), следовательно, она сходится. Ч.Т.Д.
), следовательно, она сходится. Ч.Т.Д.
Определение 5: Ряд ![]() называется
абсолютно сходящимся, если
называется
абсолютно сходящимся, если ![]() .
.
Для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают. При исследовании свойства абсолютной сходимости используют признаки сходимости знакоположительных рядов.
Теорема 3: Всякий абсолютно сходящийся ряд сходится
также и в обычном смысле, то есть ![]() сходится
сходится ![]() сходится.
сходится.
Действительно, представим исходный ряд ![]() в виде разности двух знакоположительных
рядов, для чего введем две новые последовательности
в виде разности двух знакоположительных
рядов, для чего введем две новые последовательности ![]() :
:
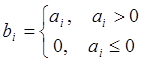
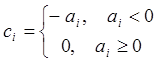 , тогда
, тогда ![]() ,
причем
,
причем ![]() .
.
Поскольку ряд 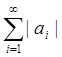 сходится по условию
теоремы, то, согласно признаку сравнения 1.1, сходятся и знакоположительные
ряды
сходится по условию
теоремы, то, согласно признаку сравнения 1.1, сходятся и знакоположительные
ряды 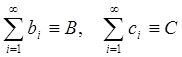 . Для частичных сумм исходного ряда имеем:
. Для частичных сумм исходного ряда имеем: 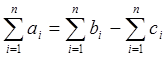 . Поскольку последовательности частичных
сумм для рядов, стоящих в правой части равенства, сходятся, то сходится и
последовательность частичных сумм исходного ряда:
. Поскольку последовательности частичных
сумм для рядов, стоящих в правой части равенства, сходятся, то сходится и
последовательность частичных сумм исходного ряда: 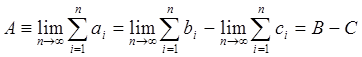 .
Ч.Т.Д.
.
Ч.Т.Д.
Отметим, что обратное утверждение не верно. Из обычной сходимости ряда не следует его абсолютная сходимость.
Пример 6: Исследовать сходимость ряда 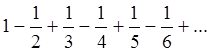
Как следует из рассмотрения примера 3, ряд не имеет
абсолютной сходимости. С другой стороны, это знакочередующийся ряд, члены
которого удовлетворяют условиям: 1) ![]() 2)
2) ![]() . Следовательно, согласно теореме Лейбница,
ряд сходится.
. Следовательно, согласно теореме Лейбница,
ряд сходится.
Как будет показано в дальнейшем,
 .
(57)
.
(57)
Определение 6: Сходящийся ряд, который не является абсолютно сходящимся, называют условно сходящимся.
Достаточно нетривиальным представляется вопрос о порядке суммирования (замене мест слагаемых) бесконечного ряда. Оказывается, что, в отличие от любых сумм с конечным числом слагаемых, изменение порядка суммирования бесконечного ряда может приводить в общем случае к изменению результата суммирования.
Теорема 4: Сумма ряда ![]() ,
сходящегося абсолютно, не зависит от порядка суммирования. Абсолютно сходящиеся
ряды называют также коммутативными.
,
сходящегося абсолютно, не зависит от порядка суммирования. Абсолютно сходящиеся
ряды называют также коммутативными.
Теорема 5 (Римана): Члены любого условно (неабсолютно) сходящегося ряда можно переставить таким образом, что ряд будет сходиться к любому наперед заданному числу или же станет расходящимся.
Пример 7: Проиллюстрируем теорему Римана на примере ряда (57).
Переставим члены ряда (57) двумя приведенными ниже способами и найдем сумму ряда, соответствующую каждому из порядков суммирования.
a)

b) 
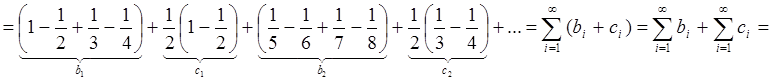
 .
.
Как видно из приведенного
примера, сумма условно сходящегося ряда (57) в зависимости от порядка
суммирования может, по крайней мере, оказаться равной ![]() ,
,
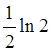 или
или 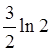 . Более
сложные перестановки членов ряда приведут к другим результатам суммирования.
Отметим, что замена местами любого конечного числа слагаемых не приведет к
изменению суммы ряда.
. Более
сложные перестановки членов ряда приведут к другим результатам суммирования.
Отметим, что замена местами любого конечного числа слагаемых не приведет к
изменению суммы ряда.
11. Число ![]() .
Экспонента
.
Экспонента
Утверждение 1: Ряд 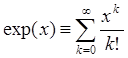 сходится абсолютно при
любом значении параметра
сходится абсолютно при
любом значении параметра ![]() .
.
Действительно, 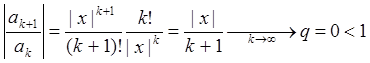 , следовательно,
согласно признаку Даламбера, ряд
, следовательно,
согласно признаку Даламбера, ряд ![]() сходится, что и
означает абсолютную сходимость ряда
сходится, что и
означает абсолютную сходимость ряда ![]() .
.
В частности, при ![]() , имеем:
, имеем: 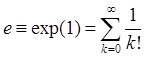 (смотри (5)).
(смотри (5)).
Утверждение 2: Последовательность 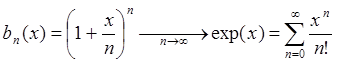 при
любом
при
любом ![]() .
.
Действительно, воспользовавшись биномиальным разложением Ньютона (27), имеем:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.