Математический анализ функции одной переменной: Учебное пособие. Часть 1 (Элементы математической логики. Множества чисел. Комплексные числа. Производная функции. Дифференциал), страница 14

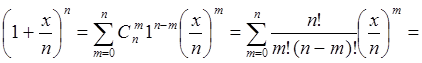
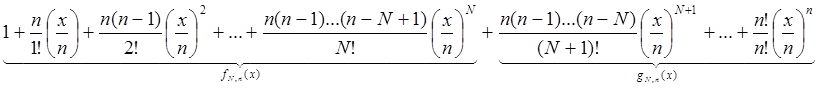Рассмотрим поведение последовательностей  и  при  для произвольного фиксированного числа  .

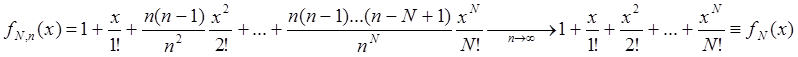
Для , где - любое постоянное число, имеем:

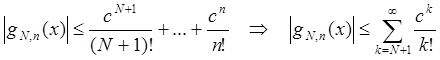 при любом .

Теперь перейдем к рассмотрению пределов при .

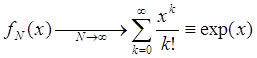
Поскольку ряд 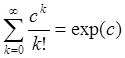 сходится,  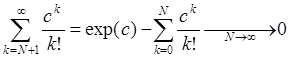(разность , где  - последовательность частичных сумм сходящегося ряда, а  - ее предел, стремится к нулю), следовательно

.

Окончательно получаем

.

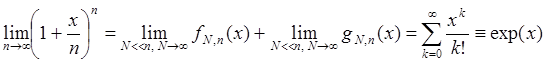В частности, при  имеем: .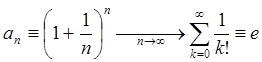

Определение 1: Основанием натуральных логарифмов называют число , которое определяется одним из двух эквивалентных способов

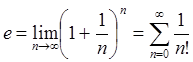.                                                           (58)

Определение 2: Экспонентой числа  называют число , которое определяется одной из двух эквивалентных формул

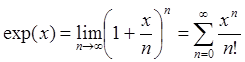.                                                       (59)

Теорема 1: При любом  числа  и  связаны формулой

.                                                                       (60)

Поскольку , для доказательства формулы (60) нужно показать, что .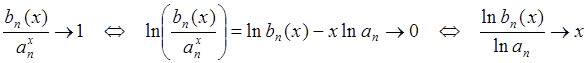

Действительно, для любого рационального  имеем ,   где .

Далее, справедливо следующее предельное соотношение

, из которого получаем

.

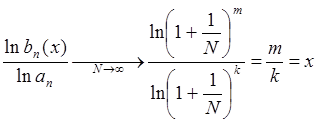Поскольку интересующий нас предельный переход доказан для всех рациональных , а любое вещественное  может быть сколь угодно точно аппроксимировано рациональным числом, мы приходим к заключению, что предельный переход верен при всех .   Ч.Т.Д.

12. Предел функции при

Для начала рассмотрим предел функции при . Определение даного предела аналогично определению предела последовательности.

Определение 1: Говорят, что функция  имеет при  предел, равный , если для любого (сколь угодно малого)  можно указать , такое что для всякого  выполняется неравенство . Пишут

   или   .                                                (61)

Как и в случае предела последовательности, графически существование у функции конечного предела, равного , означает, что график функции  имеет в области больших  горизонтальную асимптоту .

Пример 1: Найти предел функции  при .

Поскольку функция  есть показательная функция с основанием , она выходит при  на горизонтальную асимптоту  (см. рис. 7), откуда заключаем .

Помимо приведенного выше определения, можно дать эквивалентное определение предела функции при , непосредственно связанное с понятием предела последовательности.

Определение 2: Говорят, что функция  имеет при  предел, равный , если для любой последовательности  последовательность .

Отметим, что стремление  должно иметь место для любой последовательности , а не только для какой-либо определенной .

Пример 2: Исследовать существование предела функции  при .

Очевидно, что функция  не имеет горизонтальной асимптоты при , следовательно, предел у функции отсутствует.

Прийдем к аналогичному заключению с точки зрения определения 2. Не смотря на то, что существуют сходящиеся последовательности  для некоторых частных последовательностей , например

,      

,

, в общем случае произвольной последовательности  предел последовательности  будет отсутствовать. Скажем, для , последовательность

 предела не имеет.

Исключение составляют монотонные функции. Для них существование предела при  эквивалентно существованию предела  для произвольной .

Теорема 1: Пусть  есть монотонная функция и существует последовательность , такая, что , тогда .

Действительно, из существования конечного предела  следует ограниченность функции  (для неограниченных функций должно выполняться неравенство  при всех , в том числе  при , что противоречит сходимости ). Как и в случае последовательности, любая монотонная ограниченная функция имеет предел. Поскольку точки  располагаются на линии, задающей графическое представление функции , последняя должна иметь ту же самую асимптоту, что и график последовательности , то есть .     Ч.Т.Д.

Определение 3: Говорят, что функция  имеет бесконечный предел   (или ), если для любого (сколь угодно большого)  можно указать , такое что для всякого  выполняется неравенство  ().