Аналогично получается формула для производной от
котангенса ![]() .
.
Пример 7: Найти производную от ![]() .
.
Поскольку нам известна производная от ![]() , воспользуемся правилом дифференцирования
обратной функции (88):
, воспользуемся правилом дифференцирования
обратной функции (88):
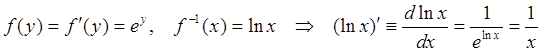 .
.
Пример 8: Найти производную от степенной функции ![]() с произвольным показателем степени.
с произвольным показателем степени.
![]() .
.
Данная формула обобщает результат примера 2 на случай степенной функции с произвольным (не обязательно натуральным) показателем степени.
Пример 9: Найти производную от функции ![]() .
.
Воспользуемся правилом дифференцирования обратной функции
(88), а также основным тригонометрическим тождеством: ![]()
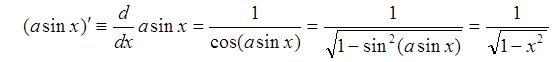 .
.
Предлагаем читателю найти
производные от функций ![]() самостоятельно. Для
удобства дальнейшего использования суммируем полученные выше результаты в виде таблицы
производных:
самостоятельно. Для
удобства дальнейшего использования суммируем полученные выше результаты в виде таблицы
производных:
Основные формулы дифференцирования:
1) ![]() 2)
2)
![]()
3) ![]() 4)
4)
![]()
5) ![]() 6)
6)
![]()
Формулы дифференцирования элементарных функций:
1)
![]()
2)
![]() 3)
3)
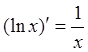
4) ![]() 5)
5)
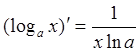
6) ![]() 7)
7)
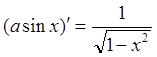
8) ![]() 9)
9)
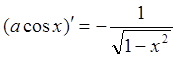
10) 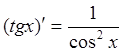 11)
11)
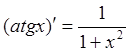
12) 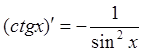 13)
13)
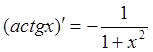
Пример 10: Найти производную от функции ![]() .
.
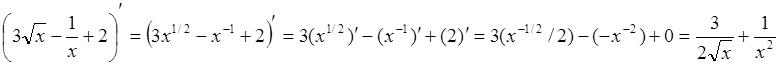 .
.
Пример 11: Найти производную от функции ![]() .
.
Воспользовавшись свойствами логарифма, получаем
![]() .
.
К аналогичному результату можно прийти, рассмотрев ![]() как композицию двух функций
как композицию двух функций ![]() и
и ![]() :
:
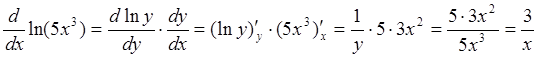 .
.
Пример 12: Найти производные от функции ![]() и
и ![]() .
.
В первом случае имеет место композиция функций ![]() и
и ![]() ,
следовательно
,
следовательно
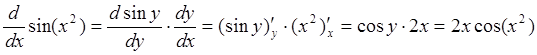 .
.
Во втором случае присутствует композиция тех же
элементарных функций, но в обратном порядке (внутренняя и внешняя функции
заменены местами) ![]() ,
, ![]() .
.
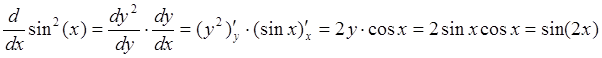
Пример 13: Найти производную от функции ![]() .
.
Простейший ход решения выглядит следующим образом:
![]() (смотри таблицу
элементарных функций).
(смотри таблицу
элементарных функций).
Другой вариант решения – воспользоваться формулой производной от частного:
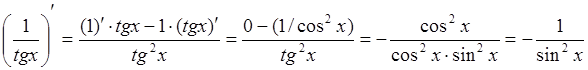 .
.
Наконец, можно рассмотреть функцию ![]() как
композицию двух функций
как
композицию двух функций ![]() и
и ![]() , тогда
, тогда
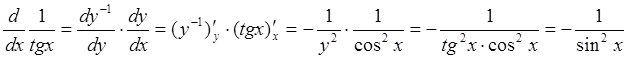 .
.
Пример 14: Найти производную от функции 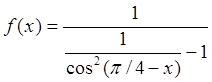 .
.
Очевидно, что данная функция представляет собой композицию
нескольких элементарных функций. Наиболее прямой (и наиболее громоздкий) способ
решения состоит в том, чтобы последовательно, начиная с самой внутренней,
определить все функции, входящие в композицию, после чего воспользоваться
формулой (87). Самой внутренней функцией композиции (той, которая в первую
очередь вычисляется при расчете на калькуляторе) является линейная функция ![]() , далее имеем:
, далее имеем: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Отметим, что, в свою очередь,
функцию ![]() можно было представить в виде композиции
двух более простых функций
можно было представить в виде композиции
двух более простых функций ![]() и
и ![]() , однако, поскольку вычисление производной
непосредственно от функции
, однако, поскольку вычисление производной
непосредственно от функции ![]() не вызывает труда, это
привело бы только к неоправданному увеличению записи решения.
не вызывает труда, это
привело бы только к неоправданному увеличению записи решения.
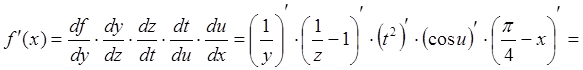
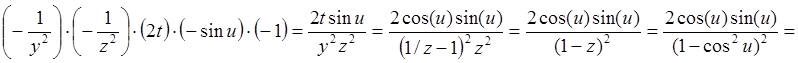
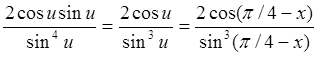 .
.
Более красивый способ решения заключается в том, чтобы
изначально упростить выражение для ![]() . Пусть, по-прежнему,
. Пусть, по-прежнему, ![]() , тогда
, тогда
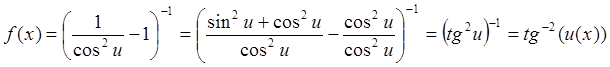 .
.
Теперь можно представить функцию ![]() как
композицию только трех функций:
как
композицию только трех функций: ![]() ,
, ![]() ,
, ![]() . Вновь
применяя формулу (87), получаем
. Вновь
применяя формулу (87), получаем
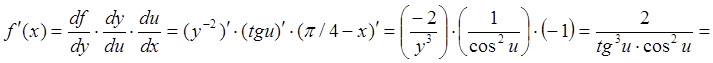
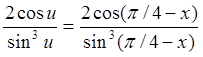 .
.
Пример 15: Найти производную от функции ![]() .
.
Известные формулы дифференцирования для степенной ![]() и показательной
и показательной ![]() функций
в данном случае не приемлемы, поскольку как основание, так и показатель степени
не являются постоянными (зависят от
функций
в данном случае не приемлемы, поскольку как основание, так и показатель степени
не являются постоянными (зависят от ![]() ). Для того чтобы свести
функцию
). Для того чтобы свести
функцию ![]() к показательной, воспользуемся основным
логарифмическим тождеством
к показательной, воспользуемся основным
логарифмическим тождеством ![]()
![]() , далее, используя правило
дифференцирования сложной функции (86), пролучаем
, далее, используя правило
дифференцирования сложной функции (86), пролучаем
![]() .
.
Аналогично может быть получена формула для
производной от произвольной функции вида ![]() :
:
![]() , в итоге имеем
, в итоге имеем
![]() . (89)
. (89)
В заключении параграфа получим формулу для
производной от функции вида ![]() :
:
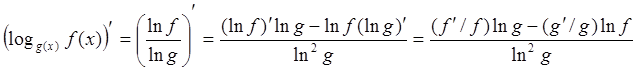 . (90)
. (90)
Пример 16: Найти производную от функции ![]() .
.
Поскольку ![]() , получаем
, получаем
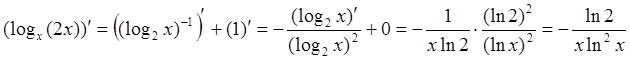 .
.
С другой стороны, этот же результат можно непосредственно получить из формулы (90):
![]()
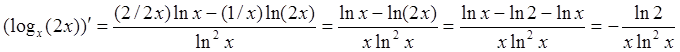 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.