Мы приходим к отрицанию условия теоремы: ![]() (
(![]() не
является несократимой дробью) Ч.Т.Д.
не
является несократимой дробью) Ч.Т.Д.
Определение 8: Если доказана истинность теоремы ![]() , то
, то ![]() называют необходимым условием для
выполнения
называют необходимым условием для
выполнения ![]() .
.
Действительно, поскольку ![]() ,
то из невыполнения
,
то из невыполнения ![]() автоматически следует, что
автоматически следует, что ![]() также не выполняется.
также не выполняется.
Определение 9: Если доказана истинность обратной теоремы ![]() , то
, то ![]() называют
достаточным условием для выполнения
называют
достаточным условием для выполнения ![]() .
.
Отметим, что необходимое и достаточное условия никогда не следуют друг из друга. Каждое из них нуждается в отдельном доказательстве.
Пример 2: ![]() Здесь
Здесь ![]() является
необходимым, но не достаточным условием для выполнения
является
необходимым, но не достаточным условием для выполнения ![]() .
.
Если верны как прямая ![]() , так и
обратная
, так и
обратная ![]() теоремы, то утверждения
теоремы, то утверждения ![]() и
и ![]() оказываются
эквивалентны
оказываются
эквивалентны ![]() , при этом
, при этом ![]() является
необходимым и достаточным условием для выполнения
является
необходимым и достаточным условием для выполнения ![]() , в свою очередь
, в свою очередь ![]() является
необходимым и достаточным условием для выполнения
является
необходимым и достаточным условием для выполнения ![]() .
.
Отметим также, что согласно Т2 доказательство
обратного утверждения ![]() можно заменить доказательством
противоположного утверждения
можно заменить доказательством
противоположного утверждения ![]() .
.
Метод математической индукции состоит в
следующем: для доказательства верности утверждения ![]() при
всех натуральных
при
всех натуральных ![]() нужно доказать, что
нужно доказать, что
1.
![]() верно при
верно при ![]() ,
,
2.
![]() при любом
при любом ![]() .
.
Пример 3: Докажем, что для ![]() - го члена и суммы
первых
- го члена и суммы
первых ![]() членов геометрической прогрессии,
которая определяется заданием первого члена
членов геометрической прогрессии,
которая определяется заданием первого члена ![]() и
рекуррентной формулой
и
рекуррентной формулой ![]() (
(![]() -
знаменатель геометрической прогрессии) имеют место следующие формулы:
-
знаменатель геометрической прогрессии) имеют место следующие формулы:
![]() ,
, ![]() (1)
(1)
1.
При ![]() имеем:
имеем: ![]() ,
, ![]()
2.
Пусть формулы (1)
верны для ![]() , докажем их верность для
, докажем их верность для ![]() :
:
![]() ,
,
 Ч.Т.Д.
Ч.Т.Д.
3. Множества чисел
Множество натуральных чисел замкнуто относительно
операций сложения и умножения (![]() ), однако не содержит
обратных по этим операциям элементов.
), однако не содержит
обратных по этим операциям элементов.
![]() - множество целых чисел
- множество целых чисел ![]() получается из
получается из ![]() добавлением
нуля и всех обратных по сложению (противоположных) элементов.
добавлением
нуля и всех обратных по сложению (противоположных) элементов.
Определение 1: Факториал целого числа ![]() определяется
формулой:
определяется
формулой:
![]()
![]() (2)
(2)
Определение 2: Двойной факториал целого числа
![]() задается формулами:
задается формулами:
![]()
![]() , если
, если ![]() - четное
- четное
![]()
![]() , если
, если ![]() -
нечетное (3)
-
нечетное (3)
![]() - множество рациональных чисел
- множество рациональных чисел
![]() , где
, где ![]() - целые
числа,
- целые
числа, ![]() получается
из
получается
из ![]() добавлением всех обратных по умножению
элементов
добавлением всех обратных по умножению
элементов ![]() с последующим «замыканием» по умножению,
то есть составлением всевозможных произведений
с последующим «замыканием» по умножению,
то есть составлением всевозможных произведений ![]() (
(![]() обратного по умножению элемента не имеет,
его аналогом является символ бесконечности
обратного по умножению элемента не имеет,
его аналогом является символ бесконечности ![]() ).
).
Теорема 1: Каждое рациональное число может быть представлено в виде конечной или бесконечной периодической десятичной дроби.
Пример 1: 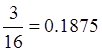 - конечная десятичная дробь с четырьмя
значащими цифрами после десятичной точки. Конечная десятичная дробь может
рассматриваться как бесконечная с периодом
- конечная десятичная дробь с четырьмя
значащими цифрами после десятичной точки. Конечная десятичная дробь может
рассматриваться как бесконечная с периодом ![]() :
: ![]()
Пример 2: 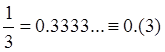 ,
, 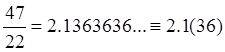 ,
, 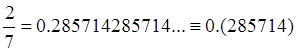 - бесконечные десятичные дроби с периодами
- бесконечные десятичные дроби с периодами
![]() ,
, ![]() и
и ![]() соответственно.
соответственно.
![]() - множество вещественных чисел
- множество вещественных чисел
![]() , где
, где ![]() получается
из
получается
из ![]() добавлением всевозможных пределов
последовательностей, составленных из рациональных чисел (понятие предела
последовательности будет рассмотрено в §10).
добавлением всевозможных пределов
последовательностей, составленных из рациональных чисел (понятие предела
последовательности будет рассмотрено в §10).
Пример 3: Дана последовательность, все члены которой ![]() ,
, ![]()
Пример 4: Дана последовательность ![]()
![]() ,
, ![]() .
Действительно, при
.
Действительно, при ![]() мы получим бесконечную
непериодическую десятичную дробь.
мы получим бесконечную
непериодическую десятичную дробь.
Определение 3: Вещественное число, которое не является рациональным (не представимо в виде периодической десятичной дроби) называют иррациональным.
Теорема 2: Всякое иррациональное число может быть с любой степенью точности аппроксимировано (приближено) рациональным числом.
Действительно, оставив в десятичной записи
иррационального числа первые ![]() цифр после десятичной
точки и заменив все последующие цифры нулями, мы получим рациональное число,
которое аппроксимирует исходное иррациональное с погрешностью
цифр после десятичной
точки и заменив все последующие цифры нулями, мы получим рациональное число,
которое аппроксимирует исходное иррациональное с погрешностью ![]() Ч.Т.Д.
Ч.Т.Д.
Пример 5: ![]() - иррациональное число (смотри пример 1,
§3)
- иррациональное число (смотри пример 1,
§3)
![]() ,
где
,
где 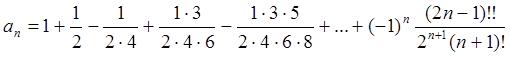 (4)
(4)
Пример 6: Основание натуральных логарифмов ![]() -
иррациональное число.
-
иррациональное число.
![]() , где
, где
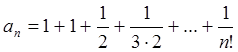 (5)
(5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.