1)
![]() 2)
2)
![]()
3)
![]() 4)
4) ![]()
5)
![]() 6)
6)
![]()
Типичные графики степенных функций
приведены на рис. 4. Область определения степенной функции зависит от
показателя степени ![]() :
:
![]()
![]()
![]()
![]()
Частными случаями суммы степенных функций являются линейная и квадратичная функции.
Определение 2: Линейной функцией называют функцию вида
![]() (34)
(34)
Графиком линейной функции
является прямая (рис. 5). Параметр ![]() определяет тангенс угла
наклона прямой. При
определяет тангенс угла
наклона прямой. При ![]() функция возрастает, при
функция возрастает, при ![]() - убывает, при
- убывает, при ![]() значение
функции постоянно (не зависит от
значение
функции постоянно (не зависит от ![]() ) и прямая располагается
параллельно оси
) и прямая располагается
параллельно оси ![]() . Параметр
. Параметр ![]() определяет параллельный сдвиг прямой (угол
наклона неизменен) вдоль оси
определяет параллельный сдвиг прямой (угол
наклона неизменен) вдоль оси ![]() . При
. При ![]() линейная функция имеет единственный корень
линейная функция имеет единственный корень
![]() .
.
Определение 3: Квадратичной функцией называют функцию вида
![]() (35)
(35)
График квадратичной функции называют параболой (рис. 6). Поскольку
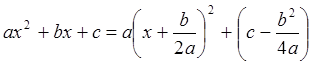 , координаты вершины параболы
(точки минимума или максимума) задаются формулами:
, координаты вершины параболы
(точки минимума или максимума) задаются формулами:
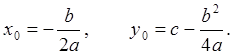 (36)
(36)
Если перенести центр координат в точку ![]() , что эквивалентно замене переменных
, что эквивалентно замене переменных
![]() , мы получим приведенный вид
уравнения параболы:
, мы получим приведенный вид
уравнения параболы:
![]() .
(37)
.
(37)
Параметр ![]() определяет скорость
изменения функции (остроту минимума или максимума). Чем больше
определяет скорость
изменения функции (остроту минимума или максимума). Чем больше ![]() , тем круче располагаются ветви параболы.
При
, тем круче располагаются ветви параболы.
При ![]() ветви параболы направлены вверх, при
ветви параболы направлены вверх, при ![]() - вниз, при
- вниз, при ![]() парабола
превращается в прямую.
парабола
превращается в прямую.
Квадратное уравнение ![]() является
алгебраическим уравнением второй степени и, следовательно, имеет два корня (в
общем случае комплексных) при любых значениях параметров. Корни легко найти из
уравнения (36):
является
алгебраическим уравнением второй степени и, следовательно, имеет два корня (в
общем случае комплексных) при любых значениях параметров. Корни легко найти из
уравнения (36):
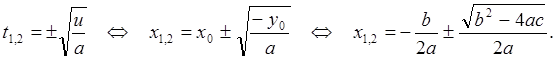
Величину ![]() называют дискриминантом
квадратного уравнения. При
называют дискриминантом
квадратного уравнения. При ![]() оба корня квадратного
уравнения вещественны и парабола пересекает ось
оба корня квадратного
уравнения вещественны и парабола пересекает ось ![]() в двух
точках. При
в двух
точках. При ![]() вещественных корней нет, и точки
пересечения параболы с осью
вещественных корней нет, и точки
пересечения параболы с осью ![]() отсутствуют. При
отсутствуют. При ![]() два вещественных корня совпадают, парабола
касается оси
два вещественных корня совпадают, парабола
касается оси ![]() в одной точке.
в одной точке.
Отметим, что функции, обратные к степенным,
также являются степенными: если ![]() , то
, то ![]() . Действительно,
. Действительно, ![]() .
.
Определение 4: Показательной функцией называют функцию вида
![]() (38)
(38)
Основные свойства показательных функций:
1) ![]()
![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
5) ![]() 6)
6)
![]()
Типичные графики показательных
функций приведены на рис. 7. Областью определения показательных функций
является вся вещественная ось. Параметр ![]() определяет
характер и скорость изменения показательной функции. При
определяет
характер и скорость изменения показательной функции. При ![]() функция возрастает, при
функция возрастает, при ![]() - убывает, при
- убывает, при ![]() значение
функции постоянно
значение
функции постоянно ![]() . Поскольку
. Поскольку ![]() , графики функций
, графики функций ![]() и
и
![]() расположены симметрично относительно оси
расположены симметрично относительно оси ![]() . Чем больше
. Чем больше ![]()
![]() , тем быстрее возрастает функция.
, тем быстрее возрастает функция.
Определение 5: Экспонентой называют показательную функцию с
основанием ![]() (см. пример 6, §4)
(см. пример 6, §4) ![]() .
Уникальность экспоненты обусловлена сохранением ее вида при дифференцировании:
.
Уникальность экспоненты обусловлена сохранением ее вида при дифференцировании: ![]() .
.
Утверждение 1: Всякая показательная функция может быть представлена в виде композиции линейной функции и экспоненты
![]() .
(39)
.
(39)
Действительно, ![]() .
.
Определение 6: Функции, обратные к показательным, называют логарифмическими функциями или логарифмами. Логарифмические функции имеют вид
![]() .
(40)
.
(40)
Основные свойства логарифмических функций:
1)
![]() (основное логарифмическое тождество)
(основное логарифмическое тождество)
2)
![]() 3)
3)
![]()
4) ![]() 5)
5) ![]()
6) ![]() 7)
7) ![]()
8) 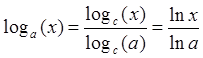 (формула замены основания) 9)
(формула замены основания) 9) 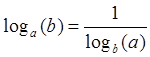
10) ![]() (обозначение натурального логарифма)
(обозначение натурального логарифма)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.