Математика \ Математика

Математический анализ функции одной переменной: Учебное пособие. Часть 1 (Элементы математической логики. Множества чисел. Комплексные числа. Производная функции. Дифференциал), страница 10

Иными словами, определение 2 означает, что какой бы узкой мы ни взяли - окрестность числа , начиная с некоторого весь «хвост» последовательности попадет в эту окрестность. Если изобразить последовательность графически, в виде набора точек с координатами (см. рис. 14а), то при достаточно больших (далеко справа) график последовательности будет ограничен сверху и снизу горизонтальными прямыми и . По мере увеличения «коридор», внутри которого располагается «хвост» последовательности становится все более узким , так что при рассмотрении в мелком масштабе все точки последовательности при больших визуально находятся на прямой (график последовательности имеет горизонтальную асимптоту ).

Определение 3: Последовательность, имеющая предел называется сходящейся. Последовательность, которая предела не имеет, называется расходящейся.

Пример 2: Найти предел последовательности .

Как видно из графика функции (рис. 4), «хвост» последовательности находится в малой окрестности точки . Тем не менее, из рисунка неочевидно имеет ли график последовательности асимптоту при больших , или же, например, асимптоту . Используя определение 2, докажем, что пределом последовательности является число .

Для любого имеем: . Если в качестве взять целую часть числа , то для любого выполняется неравенство .

(пусть для любого имеем ) Ч.Т.Д.

При рассмотрении сходящихся последовательностей можно выделить три основных типа последовательностей по способу достижения предела (см. рис. 14):

1) Убывающая (невозрастающая) последовательность, ограниченная снизу. Предел такой последовательности совпадает с ее нижней границей (при больших ).

Примеры:

2) Возрастающая (неубывающая) последовательность, ограниченная сверху. Предел такой последовательности совпадает с ее верхней границей (при больших ).

Примеры:

3) Немонотонная (осциллирующая) ограниченная последовательность, амплитуда колебаний которой (половина разности между верхней и нижней границами на интервале ) стремится к нулю при .

Примеры: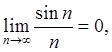

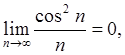
Теорема 1 (Вейерштрасса): Монотонная ограниченная последовательность имеет предел.

Теорема охватывает первые два типа последовательностей из приведенной выше классификации и имеет весьма наглядную интерпретацию: график возрастающей последовательности, ограниченный сверху горизонтальной линией, должен выйти на горизонтальную асимптоту (то же самое для графика убывающей последовательности, ограниченной снизу).

Теорема 2: (последовательность ограничена), .

Данная теорема является основной при нахождении пределов немонотонных последовательностей.

Пример 3: Найти предел последовательности .

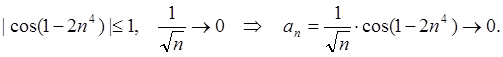
Теорема 3: Если для любого , начиная с некоторого , выполняется неравенство и существуют пределы , то выполняется нестрогое неравенство (выполнение строгого неравенства необязательно).

Теорема 4: Если для любого , начиная с некоторого , выполняются неравенства и существуют пределы , то существует . Теорема, разумеется, верна и при замене любого из неравенств (или обоих) на нестрогое.

Пример 4: Доказать, что .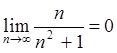

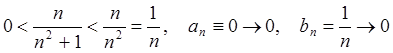(см. пример 2) 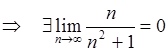Ч.Т.Д.

Определение 4: Говорят, что расходящаяся последовательность имеет бесконечный предел (или ), если для любого (сколь угодно большого) можно указать , такое что для всякого выполняется неравенство ().