Математический анализ функции одной переменной: Учебное пособие. Часть 1 (Элементы математической логики. Множества чисел. Комплексные числа. Производная функции. Дифференциал), страница 4

Если решить уравнение ,  относительно для всех значений , мы получим совокупность  различных зависимостей (функций) . В этом случае говорят, что функция  является многозначной (- значной) функцией комплексной переменной , при этом различные однозначные функции  называют ветвями функции . В ходе решения задач всегда необходимо конкретизировать о какой именно ветви многозначной функции идет речь, иными словами - в каком именно диапазоне (кратности ) находится аргумент независимой переменной.

Существуют функции с бесконечным числом ветвей. Например:

         ,   .            (17)

Степенная функция с иррациональным показателем степени также имеет бесконечное число ветвей. Действительно:

           ,    .                           (18)

Поскольку , то ни при каком  произведение .

Пример 8: Найти все значения для .

,    

Для возведения комплексного числа  в комплексную степень  нужно представить основание степени в показательной форме , а показатель степени – в алгебраической форме , тогда

  (19)

Мы видим, что неоднозначность аргумента  в общем случае приводит к неоднозначности как модуля, так и фазы функции .

Пример 9: Найти все значения для .

Этот результат можно получить непосредственно из (19), подставив    

Пример 10: Найти все значения для .

Поскольку     , непосредственно из (19) получаем:

Пример 11: Вычислить .

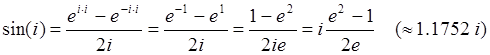
5.  Алгебраические уравнения

Определение 1: Многочленом (полиномом) степени  с комплексными коэффициентами  называют функцию вида:

                                           (20)

коэффициент  носит название свободного члена.

Определение 2: Алгебраическим уравнением степени  называют уравнение вида:

                                                                    (21)

Определение 3: Решением (корнем) уравнения  называется число  (в общем случае комплексное),  такое что .

Алгебраическое уравнение первой степени (линейное уравнение)  имеет единственное очевидное решение: .

Алгебраическое уравнение второй степени (квадратное уравнение)  всегда имеет два корня:

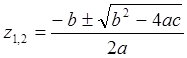,                                                          (22)

.

В том случае, если коэффициенты квадратного уравнения  вещественны, корни квадратного уравнения  вещественны при  и комплексно сопряжены  при . При  корни квадратного уравнения совпадают .

Теорема 1 (Основная теорема алгебры): Всякое алгебраическое уравнение степени  имеет  корней, некоторые из которых могут совпадать.

Иными словами, любой полином  может быть представлен в виде:

   причем  .             (23)

Число  называют кратностью корня . Корень кратности  называют простым.

Следует отметить, что при  формулы, выражающие корни алгебраического уравнения через его коэффициенты (аналогичные (22)) либо весьма громоздки и неудобны для использования (при , либо вообще не получены для всех коэффициентов (при ). Тем не менее, в ряде случаев достаточно просто найти все корни или некоторые из корней алгебраического уравнения с  используя один из следующих способов:

Первый способ - понижение степени уравнения.

Если алгебраическое уравнение содержит только степени, кратные натуральному числу :

, то путем замены переменной  степень уравнения может быть понижена в  раз.

Пример 1: Решить уравнение .

Поскольку , исходное уравнение имеет двукратный корень . Для нахождения оставшихся шести корней рассмотрим уравнение . Сделав замену переменной , получаем . По формуле (22) находим 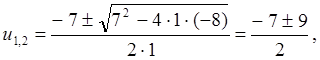      , откуда

       (см. пример 7, §5),

            

Второй способ решения алгебраических уравнений с  основывается на непосредственном использовании следующей теоремы.

Теорема 2: Если алгебраическое уравнение с целыми коэффициентами  имеет целый корень , то он является делителем свободного члена: .

Действительно, .

Пример 2: Решить уравнение .

Делителями свободного члена  являются целые числа . Проверка показывает, что  и  являются корнями уравнения (- не являются), следовательно, исходное алгебраическое уравнение можно представить в виде        

.

Для нахождения коэффициентов  поделим исходное выражение «в столбик» на