Поскольку величину ![]() можно
формально рассмотреть как функцию переменной
можно
формально рассмотреть как функцию переменной ![]() , получаем:
, получаем:
![]() , то есть приращение независимой
переменной всегда совпадает с ее дифференциалом. Что касается зависимой
переменной, то значения приращения функции
, то есть приращение независимой
переменной всегда совпадает с ее дифференциалом. Что касается зависимой
переменной, то значения приращения функции ![]() и дифференциала
и дифференциала
![]() (то есть приращения касательной), вообще
говоря, различны. Однако, при
(то есть приращения касательной), вообще
говоря, различны. Однако, при ![]() , различие между
, различие между ![]() и
и ![]() исчезает.
Данное обстоятельство достаточно очевидно уже из рассмотрения графика (рис.
21), более строгое рассмотрение имеет вид:
исчезает.
Данное обстоятельство достаточно очевидно уже из рассмотрения графика (рис.
21), более строгое рассмотрение имеет вид:
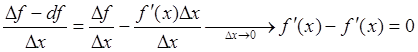 .
.
Таким образом, различие между ![]() и
и ![]() является величиной более высокого порядка
малости, чем
является величиной более высокого порядка
малости, чем ![]() , что может быть записано как
, что может быть записано как
![]() .
(78)
.
(78)
В дальнейшем, при рассмотрении ряда Тейлора, мы увидим,
что поправка ![]() имеет порядок
имеет порядок ![]() .
Обобщая вышесказанное, можем записать
.
Обобщая вышесказанное, можем записать ![]() ,
откуда следует
,
откуда следует
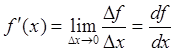 .
(79)
.
(79)
Выражение ![]() , наряду с
, наряду с ![]() и
и ![]() , используется
для обозначения производной функции
, используется
для обозначения производной функции ![]() по переменной
по переменной ![]() .
.
Формула (75) является отправной точкой для вывода различных правил дифференцирования (нахождения производных).
Теорема 1: Производная от постоянной величины равна нулю.
![]() (80)
(80)
Действительно, 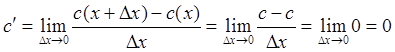 . Ч.Т.Д.
. Ч.Т.Д.
Отметим, что при дифференцировании по переменной ![]() , любое выражение, не зависящее от
, любое выражение, не зависящее от ![]() , является постоянной.
, является постоянной.
Пример 1: Найти производную функции ![]() .
.
![]()
Теорема 2: Постоянный множитель можно выносить за знак дифференцирования.
![]() (81)
(81)
Действительно, ![]()
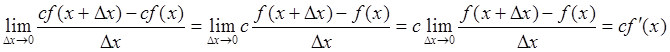 . Ч.Т.Д.
. Ч.Т.Д.
Теорема 3: Производная суммы (разности) двух функций равна сумме (разности) производных.
![]() (82)
(82)
Действительно, ![]()
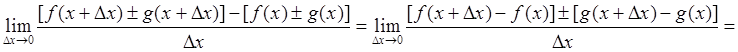
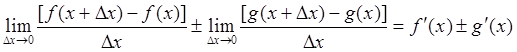 . Ч.Т.Д.
. Ч.Т.Д.
Объединение двух последних теорем дает
![]() .
(83)
.
(83)
Теорема 4: Производная произведения двух функций находится по формуле
![]() .
(84)
.
(84)
Действительно, 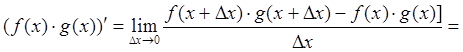
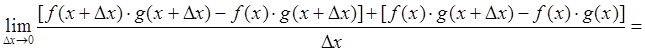
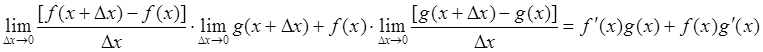 . Ч.Т.Д.
. Ч.Т.Д.
Теорема 5: Производная частного от деления двух функций находится по формуле
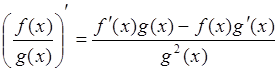 .
(85)
.
(85)
Действительно, 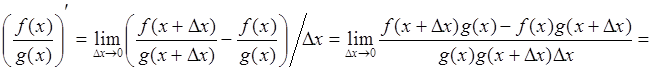
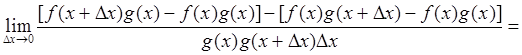
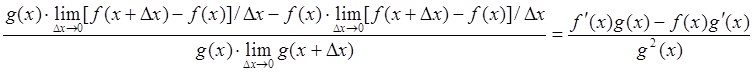 . Ч.Т.Д.
. Ч.Т.Д.
Теорема 6: Производная от композиции двух функций равна произведению производных от внешней и внутренней функций композиции по их непосредственным аргументам.
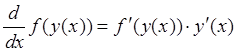 .
(86)
.
(86)
Действительно, пусть ![]() есть независимая
(внутренняя) переменная,
есть независимая
(внутренняя) переменная, ![]() - внутренняя функция
композиции,
- внутренняя функция
композиции, ![]() - промежуточный аргумент (аргумент
внешней функции),
- промежуточный аргумент (аргумент
внешней функции), ![]() - внешняя функция композиции.
Имеем:
- внешняя функция композиции.
Имеем:
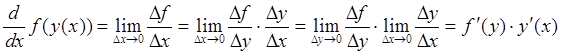 . Ч.Т.Д.
. Ч.Т.Д.
Если, в свою очередь, рассмотреть ![]() как композицию двух функций, и так далее,
Теорема 6 может быть непосредственно обобщена на случай композиции
произвольного числа функций
как композицию двух функций, и так далее,
Теорема 6 может быть непосредственно обобщена на случай композиции
произвольного числа функций
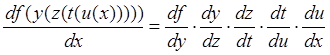 . (87)
. (87)
Формула (87) является основной для практического вычисления производных.
Теорема 7: Производная обратной функции находится по формуле
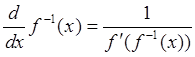 .
(88)
.
(88)
Действительно, пусть ![]() -
прямая, а
-
прямая, а ![]() - обратная функции. Продифференцировав
обе части тождества
- обратная функции. Продифференцировав
обе части тождества ![]() по переменной
по переменной ![]() , имеем:
, имеем:
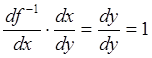 , откуда следует
, откуда следует 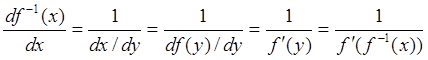 . Ч.Т.Д.
. Ч.Т.Д.
Перейдем к практическому
вычислению производных. Для начала получим значения производных от известных
нам элементарных функций.![]()
Пример 2: Найти производную степенной функции ![]() с натуральным показателем степени.
с натуральным показателем степени.
Используя определение производной (75), а также формулу Ньютона (27), получаем
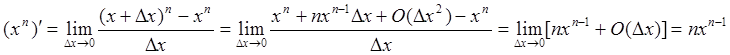 .
.
Отметим, что при ![]() данная
формула согласуется с правилом дифференцирования постоянной (80):
данная
формула согласуется с правилом дифференцирования постоянной (80): ![]() .
.
Пример 3: Найти производную от экспоненты ![]() .
.
Представив экспоненту в виде ряда (59), получаем:
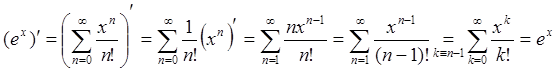 .
.
Пример 4: Найти производную от показательной
функции ![]() с произвольным основанием
с произвольным основанием ![]() .
.
Используя основное логарифмическое тождество, а также правило дифференцирования сложной функции (86), получаем:
![]() .
.
Пример 5: Найти производную от ![]() .
.
Воспользовавшись формулой Эйлера (14), имеем:
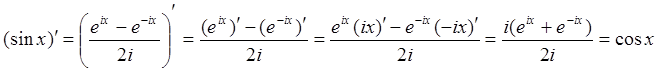 .
.
Предлагаем читателю убедиться самостоятельно, что ![]() .
.
Пример 6: Найти производную от ![]() .
.
Используя формулу производной от частного (85), получаем:
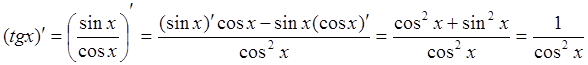 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.