Математический анализ функции одной переменной: Учебное пособие. Часть 1 (Элементы математической логики. Множества чисел. Комплексные числа. Производная функции. Дифференциал), страница 17

.                                         (71)       

Таким образом, если известно значение функции в точке  (можно вычислить ), то функция непрерывна в этой точке, при этом предел функции при  совпадает со значением функции в этой точке.

Пример 1: Найти предел функци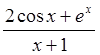и  при .  

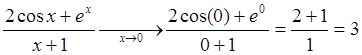
Определение 4: Говорят, что функция  непрерывна на интервале , если она непрерывна в каждой точке . Пишут .

Например, функции , равно как и их модули, непрерывны на всей вещественной оси. Графики таких функций могут быть нарисованы без отрыва ручки от бумаги.

Определение 5: Если пределы функции при  справа и слева существуют, но не совпадают, то говорят, что функция имеет в точке  разрыв первого рода (или ступенчатый разрыв). В этом случае предел при  не существует.

Пример 2: Найти точки разрыва 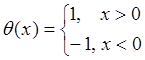функции  (см. рис. 17). Как будет показано в дальнейшем, данная функция является производной от функции .

Как следует из определения функции , значения ее без труда могут быть получены при всех . Неоднозначность (неопределенность) возникает только при . Исходя из общего определения 1, находим пределы справа и слева: . Пределы существуют, но не совпадают, следовательно, функция имеет в точке  разрыв первого рода. Нетрудно заметить, что любая функция вида , где  - непрерывная функция,  - постоянное число, имеет в точке  разрыв первого рода (вертикальную ступеньку высотой ).

Определение 6: Если предел функции при  справа или слева (или с обеих сторон) не существует, то говорят, что функция имеет в точке  разрыв второго рода. В этом случае предел при  также не существует.

Пример 3: Найти точки разрыва функции  (см. рис. 4) и определить их тип.

Как видно из графика функции, . Аналогичный результат может быть получен и на основе формулы (70): 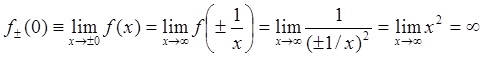. Поскольку (конечный) предел функции при  не существует, функция имеет в точке  разрыв второго рода.

Пример 4: Найти точки разрыва функции 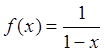 и определить их тип.

Все точки, за исключением точки  изначально принадлежат , следовательно, функция непрерывна при всех  и при всех . Исследуем поведение функции в окрестности точки . Формальная подстановка дает 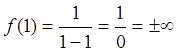. Поскольку  при  и  при , получаем: . В точке  функция имеет разрыв второго рода. График функции показан на рис. 18.

Как видно из приведенных примеров, наличие у функции бесконечного предела при  означает, что график функции выходит на вертикальную асимптоту по мере приближения к точке  справа или слева.

Пример 5: Найти точки разрыва функции  и определить их тип.

Единственной «подозрительной» на разрыв точкой является точка . Исходя из формулы (70), имеем: 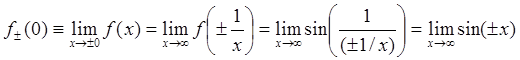. Предел как справа, так и слева не существует, соответственно, в точке  имеет место разрыв второго рода.

Для того чтобы разобраться с поведением функции  при , представим функцию в виде 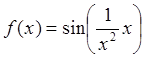. Данную функцию можно рассматривать как частный случай осциллирующей функции (42) с переменной частотой . По мере приближения  к нулю, частота осцилляций неограниченно возрастает. График функции показан на рис. 19.

Пример 6: Исследовать функцию 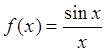 на непрерывность.

Очевидно, что данная функция определена и непрерывна при всех . Исследуем поведение функции при . Воспользовавшись формулой Эйлера (14) 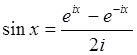, а также, представив экспоненты в виде ряда (59) 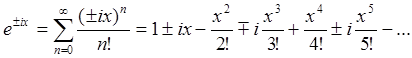, получаем представление функции  в виде ряда:

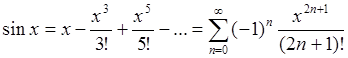.                                            (72)

Далее, поскольку 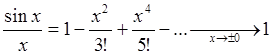, приходим к заключению, что функция непрерывна в точке , при этом ее значение в точке  следует определять согласно (71): . График функции показан на рис. 20.

В приведенном выше примере точка  изначально не принадлежит , однако значение функции в этой точке может быть доопределено «по непрерывности»: , после чего можно считать, что точка  также принадлежит  и функция непрерывна в точке . В таком случае говорят, что в точке  имеет место устранимый разрыв функции.