Математический анализ функции одной переменной: Учебное пособие. Часть 1 (Элементы математической логики. Множества чисел. Комплексные числа. Производная функции. Дифференциал), страница 18

Остановимся теперь на классификации элементарных функций по порядку малости при . Прежде всего, отметим, что все показательные функции имеют тот же порядок малости, что и постоянная величина, поскольку . Логарифмичиские функции, как было отмечено в предыдущем параграфе, также имеют один порядок малости.  

Утверждение 1: При  степенные функции с большим показателем степени имеют более высокий порядок малости (следует оставлять функции с меньшим показателем степени).

Действительно, согласно определению (70),

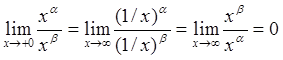 при . Смотри, также, рис. 4c.

Утверждение 2: При  логарифмические функции имеют более высокий порядок малости, чем степенные функции с показателем, меньшим нуля.

Действительно, используя определение (70), а также доказанное утверждение (64), получаем, что при всех  и  имеет место следующий предел:

.

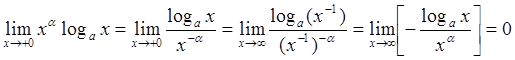  при всех  и .                                            (73)

По аналогии с предыдущим параграфом, расположим основные элементарные функции в порядке увеличения скорости возрастания их абсолютной величины при  (чем левее, тем выше порядок малости). Для функций, определенных только при  подразумевается предел справа: .

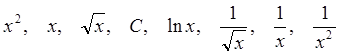.                                     (74)

Пример 7: Вычислить предел функци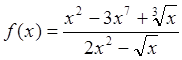и  при .

.

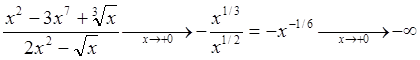Пример 8: Вычислить предел функци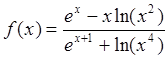и  при .

Поскольку, согласно (73), , а  (см. рис. 8), имеем:

.

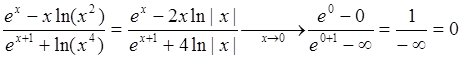14. Производная функции. Дифференциал

Понятие производной, основанное на понятии предела функции, является наиболее важным для математического анализа функций. Необходимость его возникает при попытке аппроксимировать (заменить с определенной погрешностью) некоторую функцию  линейной функцией (прямой)  на некотором интервале .

Рассмотрим произвольную гладкую (непрерывную, без острых углов) функцию , определенную в некоторой окрестности точки  (см. рис. 21). Точку  изначально предполагаем фиксированной. Поставим задачу подобрать прямую (найти уравнение прямой), которая наилучшим образом аппроксимировала бы функцию  вблизи точки . Вполне естественным представляется выбрать в качестве такой прямой касательную к графику функции  в точке . Получим уравнение касательной. Для начала напишем уравнение секущей, которая пересекает график функции  в точках  и . Как очевидно из рис. 21, 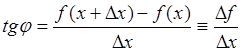. Здесь есть приращение независимой переменной (аргумента),  - приращение зависимой переменной (функции). Уравнение секущей имеет вид .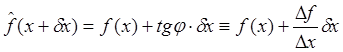

Отметим, что приращение  может принимать любые значения (разным значениям соответствуют разные точки на секущей прямой), в то время как приращение  фиксировано для данной секущей и равно разности иксовых координат точек пересечения секущей с графиком функции . В дальнейшем любое конечное приращение переменной  мы будем обозначать как , что не должно вызвать каких-либо непониманий.

По самому своему определению, касательная  получается из секущей  по мере сближения двух точек пересечения и слияния их в одну точку касания, то есть в пределе , при этом .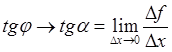

Определение 1: Тангенс угла наклона касательной к графику функции  в точке , равный пределу отношения приращения функции к приращению аргумента при , называют производной функции  в точке  и обозначают .

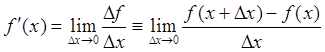                                             (75)

Уравнение касательной к графику функции  в точке  может теперь быть записано в виде

.                                                      (76)

Очевидно, что значение производной  различно для различных . Если каждой точке , для которой существует предел (75), поставить в соответствие значение , то мы получим некую новую функцию переменной , которую называют производной функции .

Определение 2: Дифференциалом функции  в точке  называют линейную часть приращения функции  в точке  (приращение касательной, см. рис. 21) и обозначают

.                                                             (77)