Математический анализ функции одной переменной: Учебное пособие. Часть 1 (Элементы математической логики. Множества чисел. Комплексные числа. Производная функции. Дифференциал), страница 3

Пример 7: Число , равное отношению длины окружности к ее диаметру, – иррациональное число.

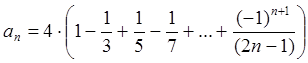,   где                                    (6)

- множество комплексных чисел    получается всевозможными сложениями двух вещественных чисел, одно из которых умножено на мнимую единицу.

Отметим, что как следует из их определения, каждое предшествующее из перечисленных числовых множеств является подмножеством последующего:

4.  Комплексные числа

Необходимость введения комплексных чисел возникает уже при решении простейшего уравнения . Если один из корней этого уравнения обозначить как  (мнимая единица), то другой корень будет равен . Мнимая единица обладает свойством , кроме того, при выполнении операций сложения и умножения, с ней можно поступать также, как с любой другой величиной (например как с  при перемножении многочленов):

                                (7)

Любое комплексное число может быть представлено в одной из трех форм записи.

Алгебраическая форма записи:

                                                                            (8)

Определение 1: Вещественное число  называют вещественной частью комплексного числа  и обозначают . Вещественное число  называют мнимой частью комплексного числа и обозначают .

Таким образом, каждому комплексному числу  может быть взаимно однозначно сопоставлена упорядоченная пара вещественных чисел  или точка на координатной плоскости  (комплексной плоскости). Вместо декартовых координат  любая точка на плоскости может быть задана полярными координатами  (смотри рис. 1), где - расстояние от центра координат до точки, - угол между осью  и направлением на точку. Легко показать, что декартовы и полярные координаты выражаются друг через друга по формулам:

,              ,                                                  (9)

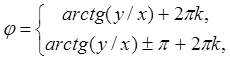
,                                                      (10)

Как мы видим, поскольку каждый поворот на  возвращает точку в исходное положение,  величина угла  определяется с точностью до , где - любое целое число. Угол  положителен при отсчете в положительном направлении (против часовой стрелки) от оси  и отрицателен при отсчете в обратном направлении.

Формулы (9) позволяют получить тригонометрическую форму записи комплексного числа:

                                                       (11)

Здесь - модуль комплексного числа, - аргумент (фаза) комплексного числа. Главное значение аргумента обычно выбирают в интервале .

Если воспользоваться формулой Эйлера

,                                                         (12)

обоснование которой будет получено нами позже, мы приходим к показательной форме записи комплексного числа:

.                                                                (13)

Отметим две весьма полезные формулы, которые непосредственно следуют из формулы Эйлера:

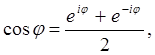
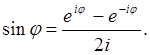                                                  (14)

Определение 2: Число  называют комплексно сопряженным к числу . Произведение числа  на комплексно сопряженное  всегда неотрицательно:

                                                   (15)

Нетрудно заметить, что при сложении и вычитании комплексных чисел более удобна алгебраическая форма записи, в то время как при умножении и делении предпочтительной является показательная форма.

Пример 1: Вычесть из комплексного числа  число .

Пример 2: Найти отношение  для  из примера 1.

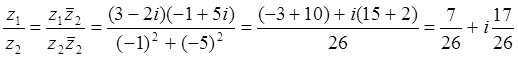
Пример 3: Записать комплексные числа  и  в показательной форме.

,      

,      

(для краткости здесь указаны только главные значения аргументов).

Пример 4: Найти произведение  для  из примера 3.

Пример 5: Найти отношение  для  из примера 3.

Пример 6:    Найти .

Пример 7: Найти все значения для  (смотри рис. 2).

,

,

,

.

Как видно из последнего примера, при вычислении нецелых степеней комплексного числа, результат вычисления может принимать ряд различных значений. Например, решая уравнение ,  относительно , мы получим  различных корней уравнения

,      ,     ,                          (16)   расположенных на комплексной плоскости  в вершинах правильного - угольника, вписанного в окружность радиуса . При  все перечисленные корни уравнения повторяются снова, новых корней не образуется.